Hace unos días estaba yo visitando el canal de YouTube del compositor minimalista estadounidense, afincado en París, Tom Johnson (Greeley, Colorado, EE.UU., 1939). En particular, estaba viendo algunos de sus videos de la serie Illustrated Music, en la que el compositor explica la manera en la que crea sus composiciones musicales utilizando conceptos matemáticos, como permutaciones, combinaciones, sucesiones numéricas, teselaciones rítmicas perfectas, el triángulo de Pascal, el problema de las estudiantes de Kirkman o diseños combinatorios, entre muchos otros (podéis leer las entradas Las vacas de Narayana, la versión hindú de los conejos de Fibonacci y Teselaciones rítmicas perfectas, para conocer las matemáticas que utiliza en dos de sus composiciones). En uno de los videos de la serie, el número 19, Tom Johnson explica su obra para guitarra Tinkelenberg Rhythms (2014) y cómo utiliza un cuadrado mágico geométrico, encontrado por el programador de software, mago matemático y creador de rompecabezas matemáticos holandés Frank Tinkelenberg, para realizar su composición musical.

Si hablamos de “cuadrados mágicos geométricos”, se ponen en juego dos cuestiones. La primera es que estamos hablando de “cuadrados mágicos”, que están relacionados con los números, y la segunda es que el término “geométricos” nos indica que se están modificando los elementos que componen los cuadrados mágicos, ya no son números. Pero vayamos por partes.

Los cuadrados mágicos son unos objetos matemáticos que han cautivado a matemáticos y no matemáticos a lo largo de la historia. Se pueden encontrar, normalmente, en libros de divulgación de las matemáticas, de matemática recreativa o incluso de magia, pero también, en libros de ajedrez (como vimos en la entrada ¿Existen recorridos mágicos del caballo en el tablero de ajedrez?). Sobre ellos investigaron grandes matemáticos como el francés Pierre de Fermat (1607-1665) o el suizo Leonhard Euler (1707-1783), y hasta personalidades como el político, científico e inventor estadounidense Benjamin Franklin (1706-1790), se atrevieron con ellos. Los cuadrados mágicos ya se conocían desde la antigüedad (quizás más allá del año 2.200 a.n.e.), y se les relacionaba con los planetas y con la alquimia, con la magia y la astrología, con la numerología, y también se utilizaban para sanar o como amuletos.

Definición: Un cuadrado mágico de orden n es una distribución de los primeros n² números sobre las casillas de un retículo cuadrado n × n, de forma que la suma de cada fila, cada columna y cada diagonal principal sea siempre la misma, la cual se conoce con el nombre de constante mágica.

Pero nada mejor que poner un ejemplo. El siguiente cuadrado mágico de orden 4 aparece en la obra Still Life with Magic Square / Naturaleza muerta con cuadrado mágico (2011) de la artista francesa Sylvie Donmoyer.

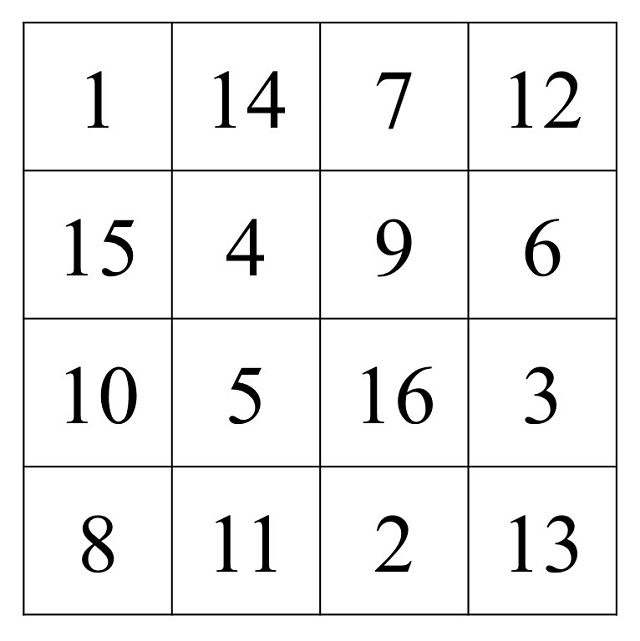
Como podemos observar la suma de los números de cada una de las cuatro filas {1, 14, 7, 12}, {15, 4, 9, 6}, {10, 5, 16, 3} y {8, 11, 2, 13}, de las cuatro columnas {1, 15, 10, 8}, {14, 4, 5, 11}, {7, 9, 16, 2} y {12, 6, 3, 13}, y de las dos diagonales principales {1, 4, 16, 13} y {8, 5, 9, 12}, es siempre la misma, 34, la constante mágica para el orden 4. Por lo tanto, la retícula cuadrada anterior es un cuadrado mágico de orden 4.

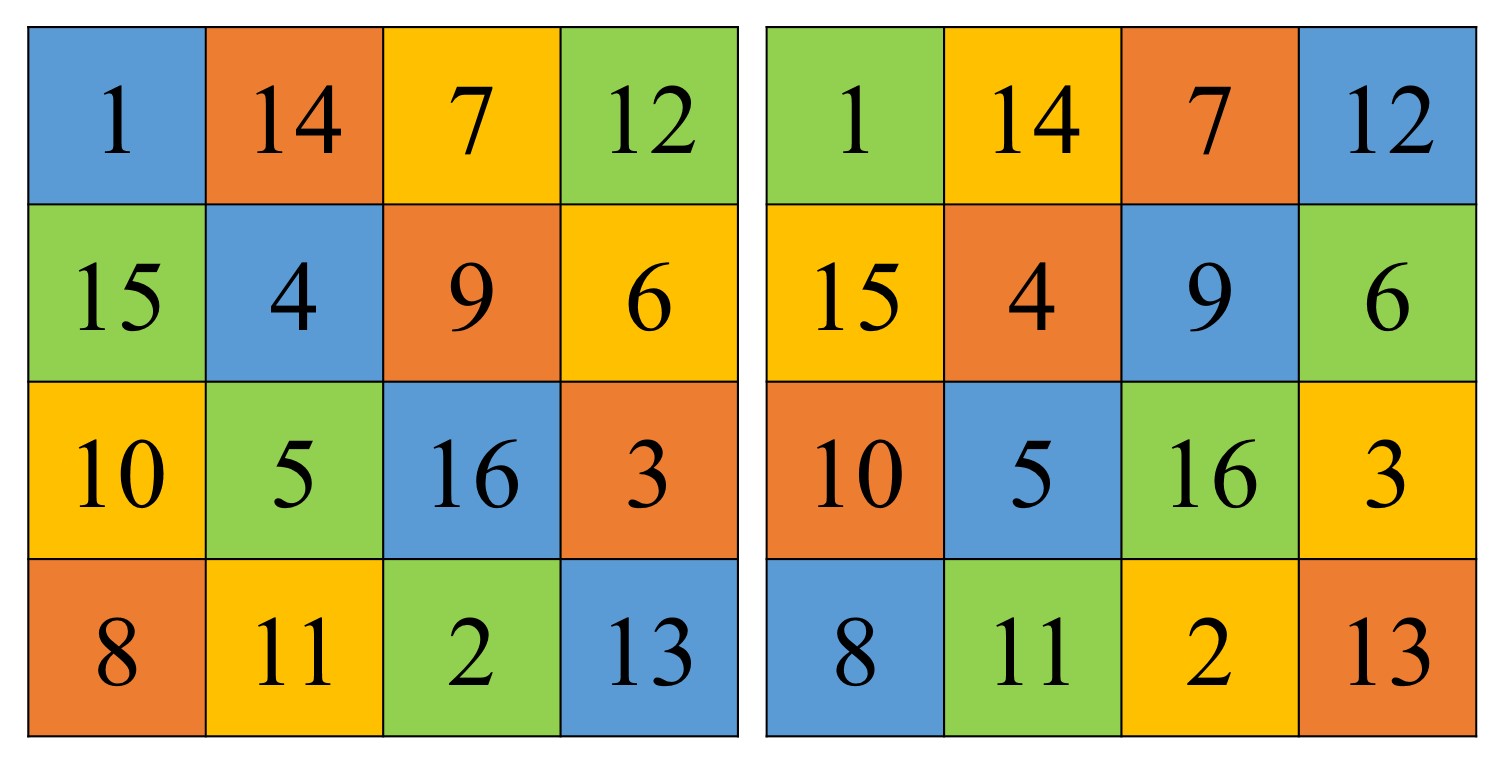
Pero este cuadrado mágico tiene más propiedades mágicas, ya que es lo que se denomina un cuadrado mágico pandiagonal (también llamados cuadrados perfectos o cuadrados panmágicos), es decir, que la suma de los números de las diagonales quebradas también es 34, como se muestra en la siguiente imagen (indicando las diagonales, en cada sentido, con colores).

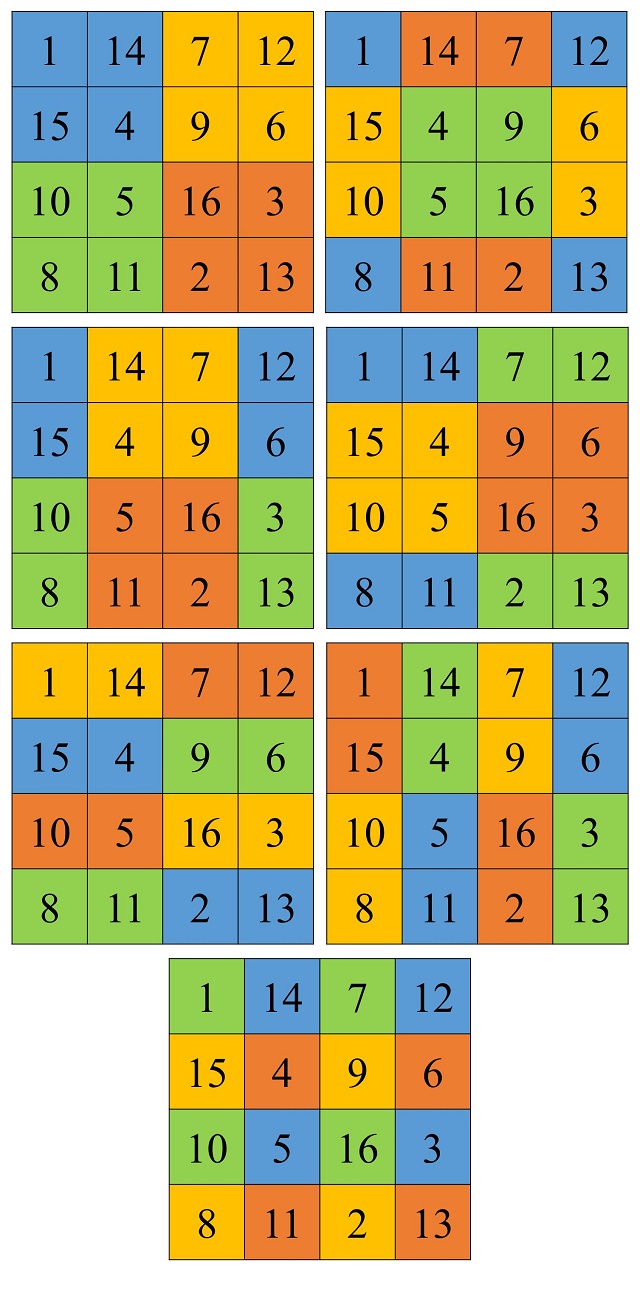
Pero aún tiene más propiedades mágicas. Veamos diferentes grupos de cuatro números que siguen sumando la constante mágica, 34. Un cuadrado mágico que cumplen todas estas condiciones (véase la siguiente imagen, en la que, de nuevo, se indica mediante colores los grupos de casillas cuya suma es 34) se dice que pertenece al grupo de cuadrados mágicos más perfectos.

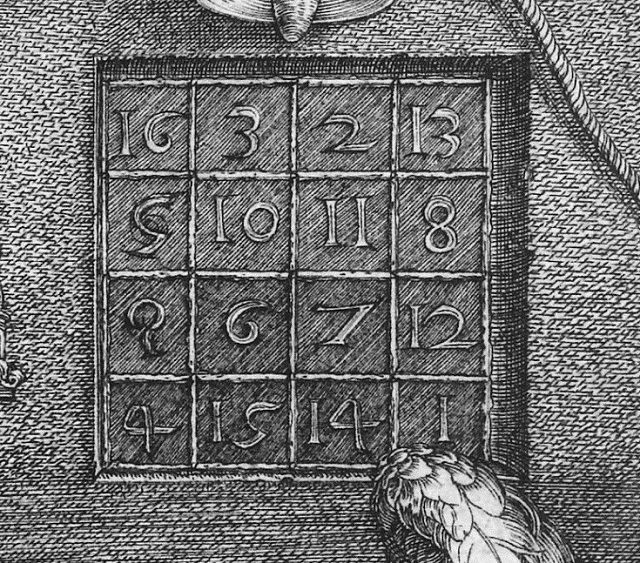
No nos olvidemos de disfrutar de la hermosa obra Still Life with Magic Square / Naturaleza muerta con cuadrado mágico (2011) de la artista Sylvie Donmoyer que recoge este cuadrado mágico.

Este es un cuadrado mágico con muchos grupos de cuatro casillas sumando la constante mágica, en este caso, 34, que como se ha comentado son las condiciones para que un cuadrado mágico sea considerado del grupo de cuadrados mágicos más perfectos. Otro cuadrado mágico famoso es el que está en el cuadro Melancolia (1514) del artista alemán Alberto Durero (1471-1528), que, si os fijáis bien, aparece en la parte superior derecha del cuadro de Sylvie Donmoyer, y que es lo que se define como un cuadrado supermágico, ya que posee también muchos grupos de cuatro casillas que suman 34, algunos grupos compartidos con los cuadrados mágicos más perfectos y otros diferentes, aunque no es pandiagonal.

Pero volvamos a los objetos que son el centro de esta entrada del Cuaderno de Cultura Científica, los cuadrados mágicos geométricos, que fueron introducidos en 2001 por el ingeniero electrónico británico, apasionado de la matemática recreativa, Lee C. F. Sallows (1944). La idea base de estos objetos es sustituir los números en el concepto de cuadrado mágico por formas geométricas.

Para entender lo que son los cuadrados mágicos geométricos, empecemos por un ejemplo sencillo.

Definición: Un cuadrado mágico geométrico (también llamado cuadrado geomágico) de orden 3 está formando por una cuadrícula 3 x 3 de formas geométricas tales que se pueden unir las formas de cada fila, cada columna o cada diagonal principal para formar la misma figura geométrica, llamada forma objetivo.

Veamos un ejemplo en el que las figuras geométricas son poliominós y la forma objetivo es un cuadrado. Recordemos (de la entrada Embaldosando con L-triominós (Un ejemplo de demostración por inducción) que un poliominó es una figura geométrica plana formada conectando dos o más cuadrados por alguno de sus lados. Los cuadrados se conectan lado con lado, pero no se pueden conectar ni por sus vértices, ni juntando solo parte de un lado de un cuadrado con parte de un lado de otro. Si unimos dos cuadrados se obtiene un dominó, si se juntan tres cuadrados se construye un triominó, o trominó, con cuatro cuadrados se tiene un tetraminó (véase la entrada Tetris, embaldosados y demostraciones), con cinco un pentominó, y así se puede continuar para cualquier número de cuadrados.

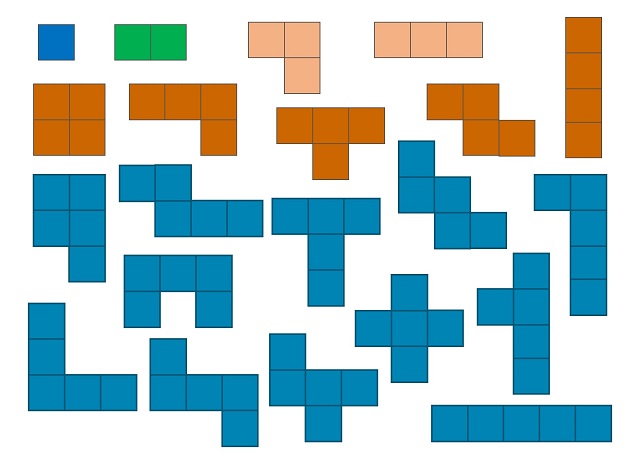
Volvamos al ejemplo de cuadrado mágico geométrico de orden 3 formado por poliominós (creado por Lee Sallows). El cuadrado mágico es el que aparece en la siguiente imagen.

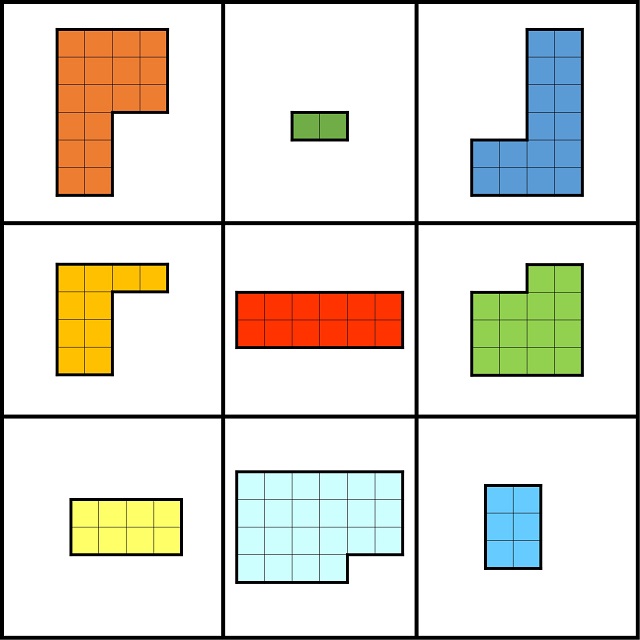
Lo forman 9 poliominós de 18, 2 y 16 cuadrados (la primera fila), de 10, 12 y 14 cuadrados (la segunda fila) y de 8, 22 y 6 cuadrados (tercera fila).

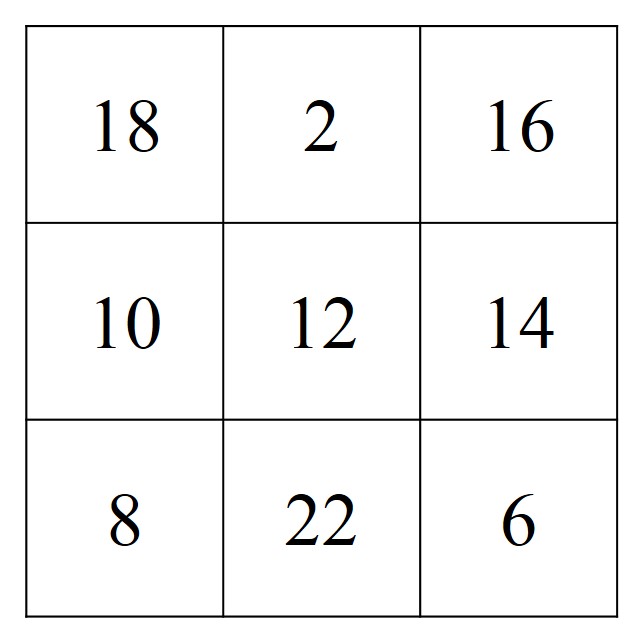
Una primera observación que podemos realizar, a partir de la definición que hemos dado, es la siguiente. Como la unión de las formas de cada fila, cada columna y cada diagonal principal es la misma (lo cual comprobaremos en breve), el número de cuadrados de todas esas uniones, que es la figura objetivo, tiene que ser la misma (de hecho, va a ser un cuadrado 6 x 6, que tiene 36 pequeños cuadrados), por lo tanto, el número de cuadrados de cada una de las figuras geométricas del retículo 3 x 3 forma un cuadrado mágico de orden 3, en sentido general, es decir, una colección de nueve números (no necesariamente los primeros nueve números) tales que la suma de las filas, las columnas y las diagonales principales es la misma. El cuadrado mágico asociado a este cuadrado mágico geométrico es el de la siguiente imagen, y su constante mágica es 36.

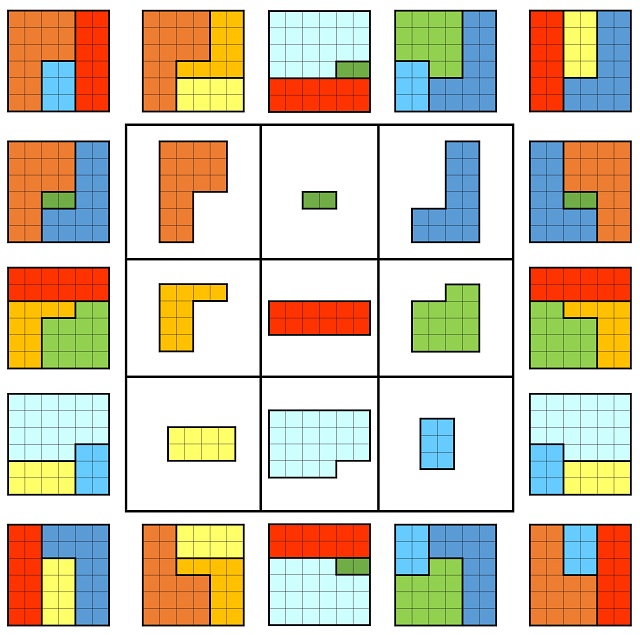
Pero veamos que efectivamente estamos ante un cuadrado mágico geométrico, mostrando la unión de cada fila, cada columna y cada diagonal principal. Para entender bien la siguiente imagen debemos de tener en cuenta dos cuestiones. La primera es que, a la hora de unir las piezas de una fila, columna o diagonal principal, las piezas pueden girarse e incluso voltearse (por ejemplo, las piezas de la tercera columna se juntan en la pieza de arriba y para ello se ha tenido que dar la vuelta a la pieza verde). Por otra parte, hemos colocado en los extremos de cada fila, columna o diagonal principal dos uniones de las tres piezas, que son una la imagen especular de la otra (como si volteamos la figura objetivo), lo cual es simplemente decorativo.

Mostremos un segundo ejemplo de cuadrado geomágico, de Lee Sallows, que aparece en un sello de Macao (China).

El “cuadrado mágico” que subyace a este cuadrado mágico geométrico es trivial, ya que el número 5 está en todas las casillas.

A continuación, mostremos un ejemplo que no está formado por poliominós, sino por los análogos con triángulos equiláteros (que Lee Sallows llama cristales mágicos, pero se suelen llamar polidiamantes), y cuya forma objetivo es un hexágono. De hecho, vamos a mostrar dos cuadrados geomágicos complementarios. En concreto, cada grupo de piezas de un color, azul y marrón, forman un cuadrado mágico geométrico en sí mismas, pero, además, las piezas azul y marrón de cada casilla se juntan dando lugar a una pieza con la misma forma en todas las casillas.

Para comprobar que efectivamente las figuras geométricas utilizadas son cristales mágicos vamos a mostrar el cuadrado mágico geométrico de las figuras marrones, pero dibujadas estas con sus triángulos equiláteros.

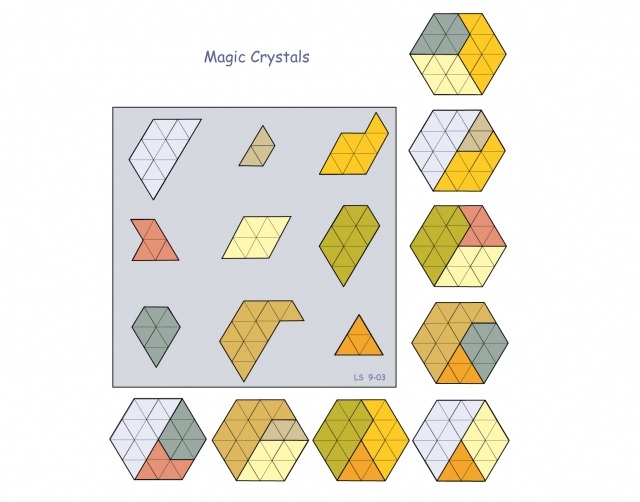
Os recomiendo que visitéis la página Geomagic Squares de Lee Sallows, que contiene una galería con 65 ejemplos de cuadrados geomágicos, algunos con curiosas propiedades. Así mismo, este autor ha publicado el libro Geometric Magic Squares: A Challenging New Twist Using Colored Shapes Instead of Numbers (Dover, 2013).

A continuación, vamos a mostrar un ejemplo de cuadrado mágico geométrico de orden 4, también de la página de Lee Sallows. Las figuras geométricas son de nuevo poliominós, más concretamente, cada línea mágica (fila, columna y diagonal principal) posee tres hexominós y un heptaminó, luego en total cada línea suma 6 x 3 + 7 = 25 cuadrados, que dan lugar a la figura objetivo, un cuadrado de tamaño 5 x 5, luego con 25 cuadrados.

Una cuestión interesante es si existen cuadrados geomágicos de orden 2. Lo primero que podemos hacer es pensar si existen cuadrados mágicos (con números) de orden 2. Supongamos que nuestro cuadrado mágico de orden 2 está formado por los números A, B, C y D. Por ejemplo, si la primera fila A y B, y la segunda fila C y D, las condiciones para que sea un cuadrado mágico son A + B = C + D = A + C = B + D = A + D = C + B. Despejando estas ecuaciones se obtiene que A = B = C = D. Es decir, la única opción para que sea un cuadrado mágico es que sea trivial, con todas las entradas iguales.

Por lo tanto, las figuras geométricas utilizadas deben tener la misma cantidad de elementos básicos. El propio Lee Sallows, en la introducción sobre cuadrados geomágicos de su página Geomagic Squares, comentaba la dificultad de encontrar un ejemplo de cuadrado geomágico de orden 2. El primero, de 2011, se debe precisamente a Frank Tinkelenberg y se muestra en la siguiente imagen. Las cuatro figuras geométricas del cuadrado geomágico son la unión de 6 secciones de un polígono de 16 lados y la figura objetivo es el polígono de 16 lados, menos 4 secciones.

Vamos a finalizar esta entrada del Cuaderno de Cultura Científica con el cuadrado mágico geométrico de Frank Tinkelenberg, que utiliza el compositor Tom Johnson para crear su pieza para guitarra Tinkelenberg Rhythms (2014), que podéis escuchar como parte del proyecto Tom Johnson for Six (parte IV) en la página de Editions 75.

El cuadrado mágico geométrico de orden 3 de Frank Tinkelenberg (del año 2011) tiene 28 grupos de tres casillas con figuras geométricas cuya unión es la figura objetivo. Recordemos que para un cuadrado geomágico de orden 3 normal se tienen exactamente 8 grupos de tres casillas (3 filas, 3 columnas y 2 diagonales principales). Para empezar, la construcción de Tinkelenberg es un cuadrado mágico geométrico pandiagonal (o cuadrado pangeomágico), ya que las diagonales quebradas también generan la figura objetivo. Así ya son 8 + 4 = 12 grupos. El resto de grupos, 28 – 12 = 16, está formado por los grupos de tres figuras geométricas que se pueden elegir en cada uno de los cuatro sub-retículos cuadrados 2 x 2. Todos ellos se pueden ver en la siguiente imagen.

Podéis entreteneros comprobando cada una de las 28 uniones de las figuras geométricas de las triadas de casillas mencionadas. Aunque, si os fijáis un poco podéis descubrir que aún hay alguna más. Según su creador, Frank Tinkelenberg, hay hasta 62 grupos distintos de tres casillas (de las C(9, 3) = 84 formas distintas de elegir tres casillas de las 9 que forman el retículo cuadrado), aunque eso yo ya no lo he comprobado.

Para finalizar, un ejemplo en el cual las figuras geométricas y la figura objetivo no son planas, sino tridimensionales. De hecho, las figuras geométricas con las que está formado el cuadrado mágico geométrico son policubos (como los poliominós, pero con cubos que se unen por sus caras) y la figura objetivo es un cubo 3 x 3 x 3 (luego formado con 27 cubos).

Bibliografía:

1.- Tom Johnson, Finding Music Writtings – Schriften, MusikTexte, 2019.

2.- Lee Sallows, Geometric Magic Squares, Mathematical intelligencer, vol.33, n. 4, pp. 25-31, 2011.

3.- Lee Sallows, Geomagic Squares

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica