En junio de 2021 la galería virtual CHDF, creada por Sylvain Clot, publicó en su cuenta de Instagram la siguiente imagen, en la cual aparecía una obra de la artista concreta suiza Suzanne Daetwyler (1948).

En esta pintura aparece representado un objeto geométrico que se conoce con el nombre de espiral de Baravelle. Sobre ella vamos a hablar en esta entrada del Cuaderno de Cultura Científica.

Primero, veamos cómo se construye la espiral de Baravelle que aparece en la obra de Suzanne Daetwyler. Se parte de un cuadrado. Después se unen los puntos medios de sus lados consecutivos mediante segmentos rectos, dibujándose así un nuevo cuadrado dentro del anterior, luego más pequeño, pero girado y que forma un rombo. De esta manera el cuadrado original queda dividido en cuatro triángulos isósceles apoyados en los vértices de ese cuadrado y el cuadrado más pequeño, con forma de rombo, que se acaba de crear. A continuación, con el nuevo cuadrado (el rombo de lados iguales) se realiza la misma operación, que da lugar a un nuevo cuadrado más pequeño dentro del anterior, pero en la misma posición que el inicial, junto a cuatro triángulos isósceles apoyados en los vértices del rombo. Y se puede continuar con este procedimiento geométrico tantas veces como se desee, hasta el infinito, obteniéndose una familia encajonada de cuadrados, como en la siguiente imagen, en la que hemos realizado seis veces la anterior construcción.

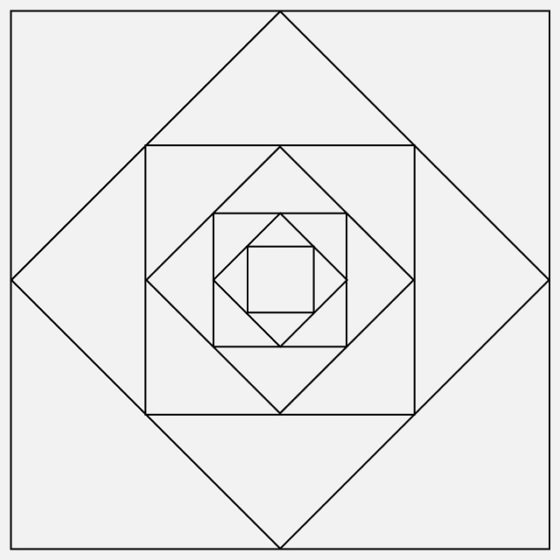
Para obtener la espiral (o espirales) de Baravelle se pintan del mismo color ciertos triángulos isósceles. En concreto, se parte de uno de los triángulos isósceles del cuadrado inicial, los más grandes, y se pinta del mismo color un triángulo isósceles de cada uno de los pasos, es decir, de cada tamaño, pero siempre en una posición girada 45 grados respecto al anterior, para crear la sensación de espiral. Al realizar la construcción geométrica anterior de forma infinita se obtendría la espiral de Baravelle (ideal), aunque normalmente se representa solo una serie finita de pasos. En la siguiente imagen se muestra la espiral de Baravelle pintada en escala de grises (realizada con seis pasos).

El diagrama anterior puede ser considerado una demostración visual (de esas demostraciones sin palabras de las que hemos hablado en más de una ocasión, como en las entradas Pitágoras sin palabras, Matemáticas para ver y tocar, Más matemáticas para ver y tocar, Teoremas geométricos sin palabras: Viviani, Teoremas geométricos sin palabras: Conway, Teoremas geométricos sin palabras: Herón o Teoremas geométricos sin palabras: Snover) de la suma de una serie infinita. En concreto, si nos fijamos en la espiral formada por los triángulos negros y consideramos que el cuadrado inicial tiene área igual a 1, entonces el triángulo isósceles negro más grande tiene un área de 1/8, ya que podemos dividir la superficie del cuadrado más grande en 8 copias de ese triángulo (las cuatro copias de las esquinas, más las cuatro copias en las que se puede dividir el rombo, que junto a los cuatro triángulos anteriores ocupan el cuadrado grande), el segundo (en tamaño) triángulo isósceles negro tiene un área de 1/16, ya que necesitamos 8 triángulos isósceles para llenar el rombo, que es la mitad del cuadrado original (o equivalentemente, necesitamos 16 triángulos isósceles de este segundo tamaño para cubrir el cuadrado grande), el tercer triángulo isósceles negro tiene un área de 1/32, y así podemos continuar hasta el infinito. Como así queda cubierta la cuarta parte del cuadrado grande (la espiral negra) se deduce la serie infinita siguiente:

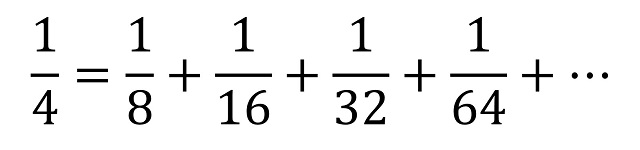
Equivalentemente, si pensamos en las cuatro espirales, que cubren todo el cuadrado original de área 1, tenemos la serie:

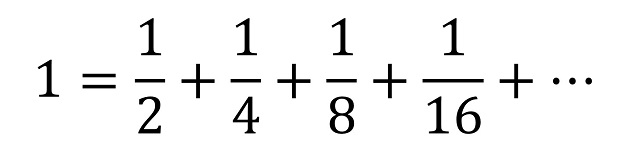
Otro artista que ha hecho uso de la anterior construcción geométrica en sus obras de arte ha sido el constructivista alemán Kunibert Fritz (1937). Desde la década de 1960 este artista ha trabajado con la construcción geométrica asociada a la llamada espiral de Baravelle, pero dando color a los triángulos de diferentes formas y creando diferentes estructuras asociadas. En la siguiente imagen se muestra una vista de la exposición Kunibert Fritz: Unidad en la dualidad en el Museo Vasarely de Budapest (17/09/2022-19/03/2023), en la cual se ven tres de estas obras.

Pero volvamos a la espiral de Baravelle. Esta familia de espirales puede ser definida para cualquier polígono regular, como el triángulo equilátero, el cuadrado, el pentágono, el hexágono, así hasta cualquier número de lados.

En la siguiente imagen vemos el resultado de la construcción geométrica para el triángulo equilátero, tras realizar cinco pasos en la construcción.

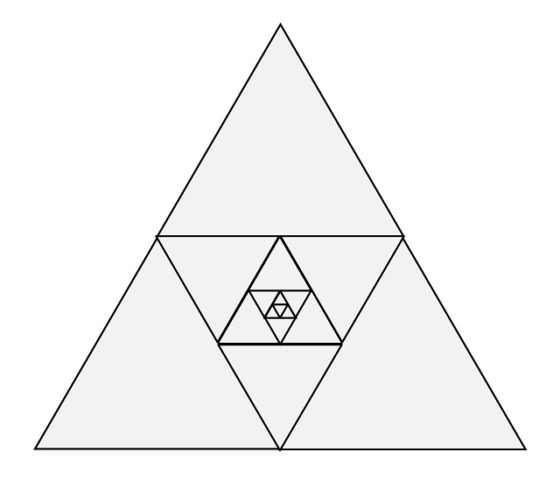
Si ahora pintamos las espirales de Baravelle (en este caso utilizamos tres colores, verde, azul y rojo, y los bordes de cada triángulo pintados del color del triángulo), queda la siguiente imagen, de una cierta belleza.

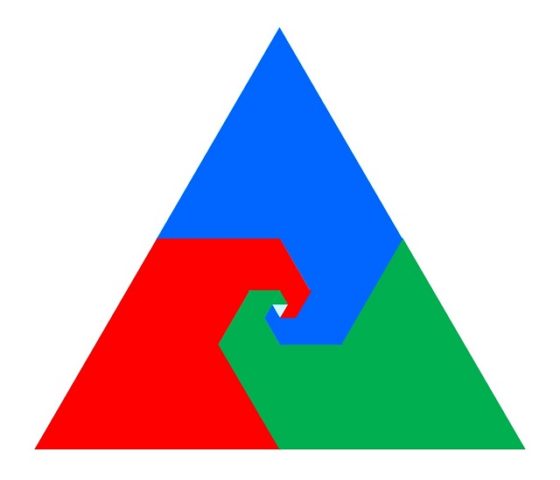
Al igual que en el caso de la espiral empezando en un cuadrado, ahora la imagen anterior puede ser considerada una demostración visual para la siguiente serie infinita.

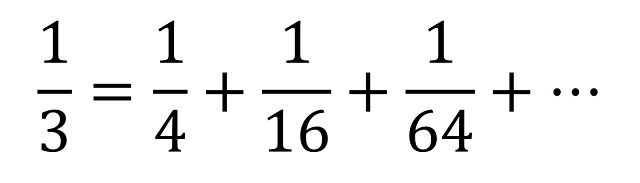
Y podemos continuar con la construcción para el pentágono, es decir, el polígono de cinco lados. En la siguiente imagen se muestra la espiral (o espirales) de Baravelle para el pentágono, después de catorce pasos.

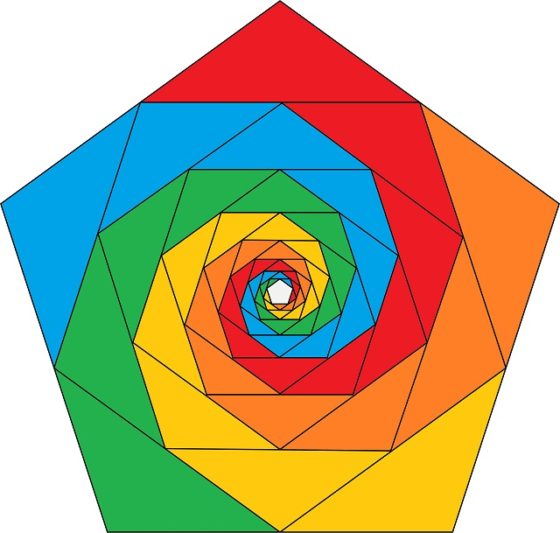
Por otra parte, a partir de la espiral de Baravelle del triángulo, el cuadrado o el hexágono se pueden hacer diseños planos más sofisticados, puesto que, con el triángulo, el cuadrado y el hexágono se puede embaldosar el plano.

Por ejemplo, con el triángulo podemos construir diseños como el siguiente:

O este otro:

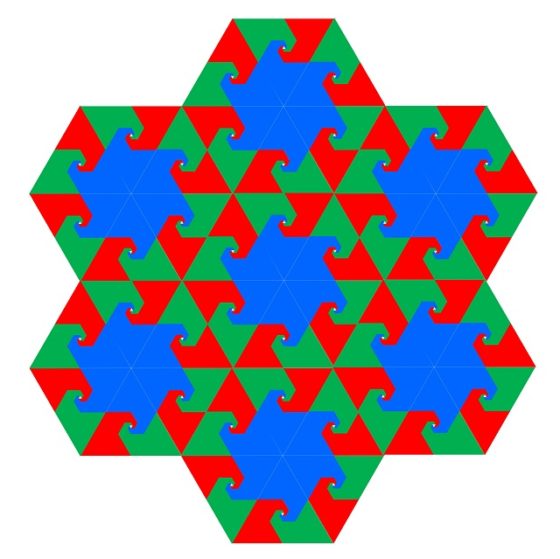
Con cuadrados he realizado este diseño, inspirado en una idea que encontré en internet.

Empezábamos esta entrada con un ejemplo de la aparición de la espiral de Baravelle en las artes plásticas, pero un campo de las artes en las que nos las encontramos también es el arte textil, en concreto en la realización de quilts.

Buscando información sobre el origen del nombre de esta artística espiral, me he topado con el pedagogo, matemático, físico y astrónomo suizo Hermann von Baravalle (1898-1973) que enseñó matemáticas dentro de la HfG – Hochschule für Gestaltung, conocida como la Escuela de Ulm, que fue una escuela universitaria de diseño en Ulm (Alemania) fundada por el artista, diseñador gráfico y tipógrafo suizo Max Bill (1908-1994), la escritora alemana Inge Aicher-Scholl (1917-1998) y el diseñador gráfico y tipógrafo alemán Otl Aicher (1922-1991). Dentro de las matemáticas enseñadas por Baravalle en la HfG, así como en algunos de sus libros, nos encontramos muchos tipos de espirales, en particular, las que hemos mostrado en esta entrada del Cuaderno de Cultura Científica. Por ejemplo, en su libro Geometrie als Sprache der Formen / La geometría como lenguaje de las formas (1963) aparecen estas espirales construidas para el cuadrado, hexágono y el octógono.

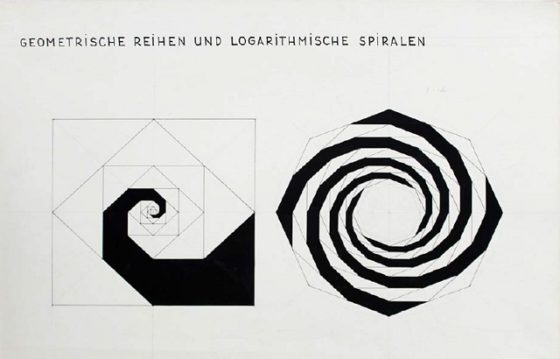
Aunque no he encontrado una referencia directa a que el nombre de la espiral de Baravelle provenga de este matemático y pedagogo, aunque su apellido es Baravalle y no Baravelle, es bastante probable que así sea.

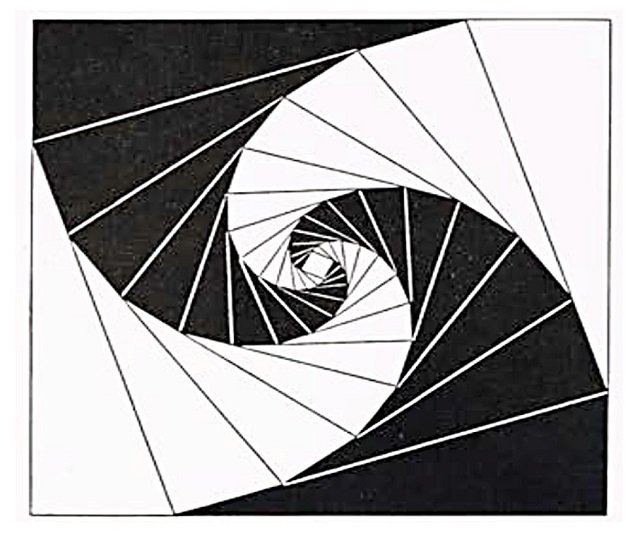
Me gustaría terminar con otra imagen del libro La geometría como lenguaje de las formas de Baravalle, en la cual vemos que la anterior construcción geométrica puede realizarse también tomando, no los puntos medios de los lados, sino otros puntos de los lados, por ejemplo, los que están a una distancia igual a un tercio de un vértice y dos tercios del otro.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica