La sucesión de Fibonacci, es una sucesión de números (naturales) que ha superado la frontera de las matemáticas, de la ciencia, para colarse en el mundo de las artes y la cultura. Que una familia de números como esta haya despertado el interés no solo dentro de la comunidad matemática, sino de toda la sociedad, se debe, en gran medida, a que juega un papel fundamental en el estudio de la morfología de las plantas, en concreto, en la filotaxis, siendo el número de espirales de las cabezas de los girasoles, las piñas o el romanescu, números de dicha sucesión, así como por su relación con el número de oro.

Por supuesto, este interés por la sucesión de Fibonacci se ha trasladado al Cuaderno de Cultura Científica, en el que hemos dedicado una cierta cantidad de entradas a la misma: Póngame media docena de fibonaccis; Una de mates: la sucesión de Fibonacci; Los números (y los inversos) de Fibonacci; Nos encanta Fibonacci; El origen poético de los números de Fibonacci; Poemas Fibonacci; La sucesión de Fibonacci, el teorema de Zeckendorf y un poemario magistral o El árbol de Fibonacci.
En esta entrada vamos a mostrar que los números de Fibonacci pueden aparecer en lugares de lo más curiosos e inesperados, además de los ya mencionados en las entradas anteriores, como solución al desafío matemático de los conejos del Liber Abaci / Libro del Ábaco (1202), del matemático italiano Leonardo de Pisa (1170-1241), conocido como Fibonacci, relacionados con la poesía en la lengua sánscrita en la India, o en la botánica, por ejemplo, en las espirales de los girasoles y piñas, o en la disposición helicoidal de las hojas en el tallo.
Los números de Fibonacci
Antes de adentrarnos en este paseo por diferentes manifestaciones de la sucesión de Fibonacci, recordemos brevemente esta sucesión, de forma directa a través de su propiedad numérica, sin entrar en el problema de los conejos, ni en la poesía en sanscrito. La sucesión de Fibonacci es una sucesión de números Fn que tiene la particularidad de que cada término es igual a la suma de los dos anteriores, Fn = Fn – 1 + Fn – 2, siendo los dos primeros términos F1 = F2 = 1.
Podemos calcular los primeros términos de la sucesión de forma sencilla, ya que cada número es la suma de los dos anteriores. De manera que los 40 primeros números de esta sucesión son:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1.597, 2.584, 4.181, 6.765, 10.946, 17.711, 28.657, 46.368, 75.025, 121.393, 196.418, 317.811, 514.229, 832.040, 1.346.269, 2.178.309, 3.524.578, 5.702.887, 9.227.465, 14.930.352, 24.157.817, 39.088.169, 63.245.986, 102.334.155, …
Esta sucesión aparece bajo la denominación A000045 dentro de La enciclopedia on-line de las sucesiones de números enteros.
Existe una organización matemática internacional, The Fibonacci Association / La asociación Fibonacci, formada por personas del ámbito de las matemáticas y de la ciencia, pero también personas amateurs interesadas en esta curiosa sucesión de números, así como en otras sucesiones relacionadas (por ejemplo, la sucesión de Lucas, con la misma propiedad recurrente, pero con los dos primeros términos L1 = 1 y L2 = 3, por lo tanto, se continua con los números 4, 7, 11, 18, 29, etcétera). Esta sociedad publica una revista, The Fibonacci Quarterly, y organiza un congreso internacional cada dos años.

Tanto la organización como la revista fueron fundadas en 1963 por el matemático estadounidense Verner E. Hoggatt (1921-1980), profesor de la San Jose State University, que era conocido como el “Profesor Fibonacci” por sus amigos y colegas, y el educador, fotógrafo y matemático estadounidense Alfred Brousseau (1907-1988), profesor en el College Saint Mary de California, a quienes unía una gran amistad y que se reunían frecuentemente para discutir sobre los números de Fibonacci, así como para cantar canciones inventadas por ellos.
El árbol genealógico de un zángano
Para empezar, vamos a mostrar dos ejemplos relacionados con las abejas en los que aparecen los números de Fibonacci. En el primero surgen estos números como las diferentes generaciones del árbol genealógico de las abejas macho, los zánganos.
Las abejas, al menos las de la especie más conocida, la abeja melífera o doméstica, son animales sociales que viven todas juntas en colmenas. Hay tres tipos de abejas en una colmena, una abeja reina, los zánganos, que son abejas macho, y las abejas trabajadoras, que son abejas hembra.
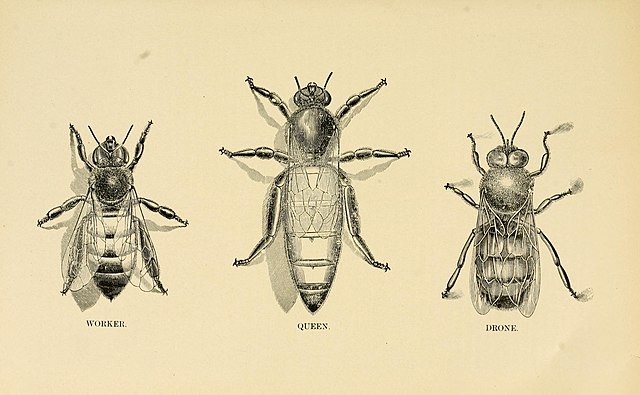
Normalmente solo hay una abeja reina en una colmena, que se encarga de las tareas reproductivas de la colonia, poniendo del orden de 1.500 huevos al día. Las abejas reina viven entre dos y tres años, aunque pueden llegar a vivir hasta cinco años. El número de zánganos de una colmena está entre unos cientos y mil, y su trabajo es también reproductivo, ya que se dedican a copular con la reina durante el vuelo de apareamiento de esta, con el fin de que los huevos sean fecundados. Los zánganos mueren cuando depositan su semen en el aparato reproductor de la abeja reina. Solamente son útiles durante la época de apareamiento, que se produce cuando hace buen tiempo (primavera y verano), no pueden picar ya que no tienen aguijón y no ayudan con ninguna otra labor de la colmena. Por este motivo, cuando llega el mal tiempo, las abejas trabajadoras expulsan a los zánganos de la colmena, que mueren de hambre y frío. Mientras que son las abejas trabajadoras, de las cuales hay unos miles en cada colmena, las que se dedican a realizar todas las tareas de la misma. La vida de las abejas obreras es de entre 5 y 6 semanas en época de buen tiempo, mientras que es de entre 5 y 6 meses si viven cuando hace mal tiempo, mientras que la de los zánganos es de entre 4 y 8 semanas.
Una de las curiosidades de la reproducción de las abejas es que las abejas macho, los zánganos, nacen de huevos no fecundados, luego solamente tienen madre, la abeja reina, mientras que las abejas trabajadoras nacen de huevos fecundados, luego tienen padre y madre. Además, la reina puede controlar si un huevo es, o no, fecundado. Las abejas trabajadoras suelen ser estériles, la mayoría de los ovarios de las trabajadoras están poco desarrollados y no producen huevos. En el caso de que una obrera tenga ovarios desarrollados, solo pondrá huevos no fecundados, luego nacerán zánganos, aunque las demás abejas trabajadoras pueden reconocer que el huevo no es de la reina y se lo comerán, salvo que la reina haya muerto y no se pueda criar otra reina, aunque eso llevará al final de la colmena, ya que no nacerán abejas trabajadoras, solo zánganos.
Este sistema de determinación del sexo del animal se llama haplodiploidía y es un sistema que no solamente se da en las abejas, sino también en otros animales, entre ellos, hormigas, avispas y algunos escarabajos.

Pero vayamos con el árbol genealógico de un zángano (1), como el que aparece en la anterior imagen. Como se ha comentado, esta abeja macho tendrá solo madre, por lo que la primera generación hacia atrás del zángano consistirá en una abeja (1), normalmente la abeja reina. Como esta abeja es hembra tendrá madre y padre (la abuela y el abuelo del zángano), luego la segunda generación del zángano serán dos abejas (2). En la tercera generación estarán la madre y el padre de la abeja abuela, así como la madre de la abeja abuelo, en total tres abejas (3). Y así se puede continuar, como se muestra en el siguiente esquema.
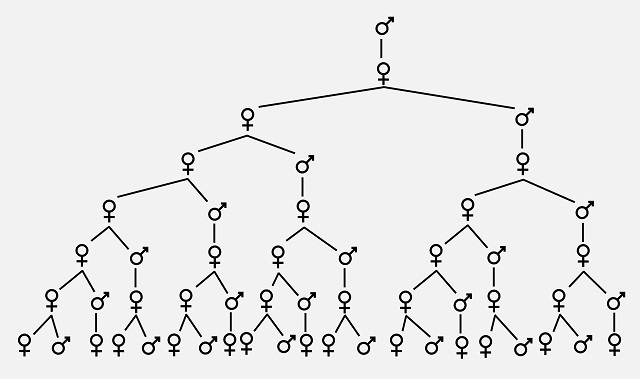
En la siguiente tabla se recogen la cantidad de abejas de cada generación hacia atrás de una abeja macho, un zángano, añadiendo además cuántas de ellas son abejas macho y cuántas abejas hembra.
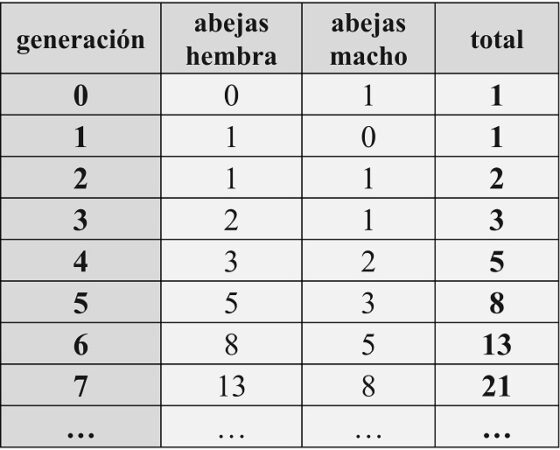
Como se observa la cantidad de abejas del árbol genealógico de un zángano, por generaciones hacia atrás, es 1, 1, 2, 3, 5, 8, 13, 21, etcétera, es decir, la sucesión de Fibonacci. Más aún, si dividimos la cantidad de abejas de cada generación, en abejas hembra y abejas macho, seguimos obteniendo esta sucesión en los dos casos.
Una paseo hexagonal
El siguiente ejemplo en el que se puede encontrar a los números de Fibonacci relacionados con las abejas se debe al matemático estadounidense Leonard Carlitz (1907-1999), de la Duke University, que fue miembro de La asociación Fibonacci y del comité editorial de la revista The Fibonacci Quarterly, en la que publicó 72 artículos, dentro de una extensa obra matemática compuesta de 771 artículos.
Imaginemos un panal de abejas, que recordemos que está formado con celdas prismáticas hexagonales pegadas unas a otras por sus caras laterales, pero con la particularidad de que está formado por tan solo dos filas de celdas, como se muestra en la siguiente imagen. En la primera celda, de uno de los extremos del panal (en la imagen en la izquierda), hay una abeja e imaginemos también que el panal es tan largo (hacia la derecha en la imagen) como queramos, de hecho, imaginemos que es infinito. Nos gustaría calcular la cantidad de caminos que puede recorrer la abeja para ir de su posición inicial a otra celda cualquiera que fijemos, desde la primera al lado de la abeja en adelante, teniendo en cuenta que de cada celda puede pasar a una contigua, pero siempre hacia delante, por ejemplo, de su celda inicial puede pasar a las celdas C1 o C2, mientras que de la celda C3 puede pasar a las celdas C4 y C5, pero no ir para atrás a las celdas C1 y C2.
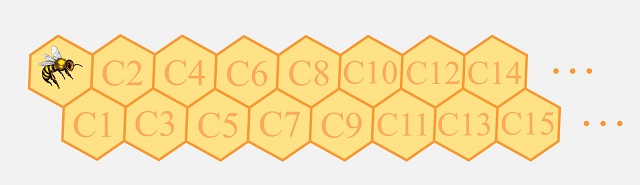
Pero vayamos contando los diferentes caminos que puede recorrer la abeja, en función de cuál sea la celda final, empezando por la celda C1 y siguiendo en orden. Solo existe una forma (1) de llegar a la celda C1, sin retroceder, que es directamente. Para llegar a la celda C2 puede hacerse directamente o a través de la celda C1, luego de dos formas (2) distintas. Y hay tres caminos posibles para alcanzar la celda C3, como se muestra en la siguiente imagen.
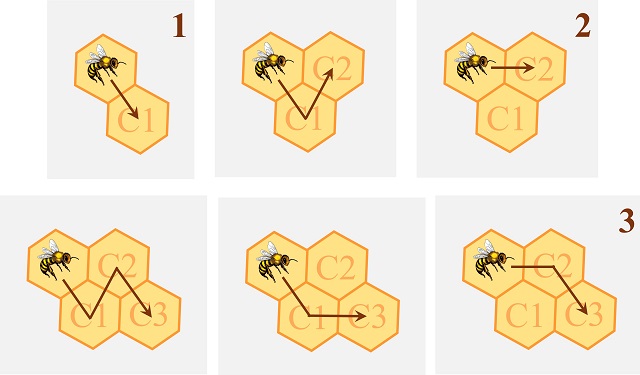
Para llegar a la celda C4 hay 5 recorridos posibles, que se muestran en la siguiente imagen.
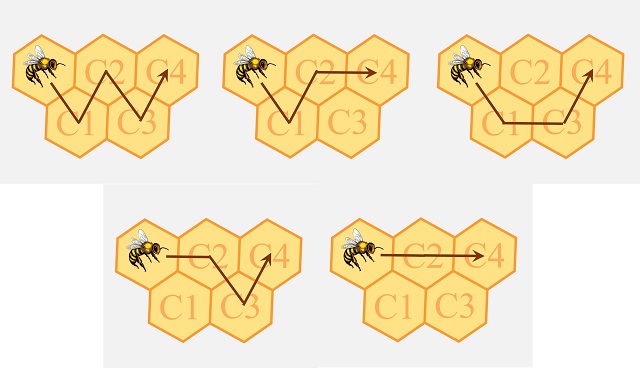
La cantidad de caminos posibles para cada una de las celdas mencionadas es 1, 2, 3 y 5, que son los primeros números de la sucesión de Fibonacci. Si seguimos con las celdas C5, C6, C7, etcétera, se irán obteniendo los demás números de la sucesión, 8, 13, 21, etcétera.
Jugando con las fichas de dominó
Para la siguiente situación vamos a considerar fichas de dominó, como la de la siguiente imagen.

Las fichas de dominó son el doble de largo que de ancho, como si juntáramos dos cuadrados. La cuestión que nos ocupa es la siguiente.
Problema: ¿de cuántas formas distintas se puede crear un embaldosado rectangular de dos filas y n columnas (es decir, una cuadrícula rectangular de tamaño n x 2), para n = 1, 2, 3, etc?
Empecemos con los casos más sencillos, para 1, 2 y 3 columnas, que se obtienen las siguientes 1, 2 y 3 formas de embaldosar, respectivamente, como se muestra en la imagen.
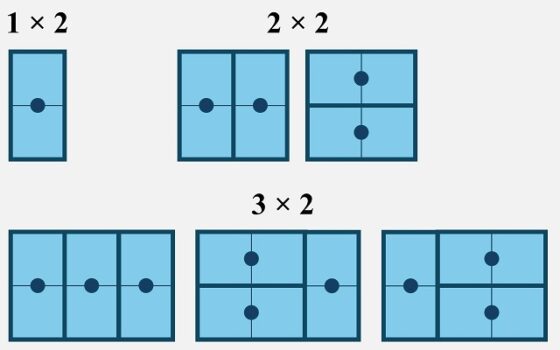
Para 4 filas empezamos a tener más maneras diferentes de colocar las fichas de dominó, en concreto 5.
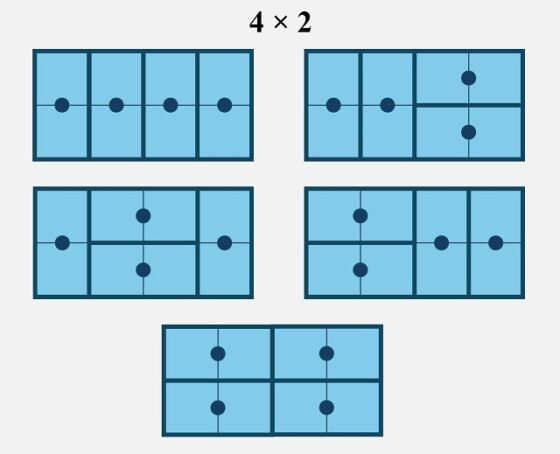
Si la cuadrícula rectangular es de tamaño 5 x 2, existen 8 formas distintas de embaldosar esta cuadrícula con fichas de dominó, como aparece en la siguiente imagen.
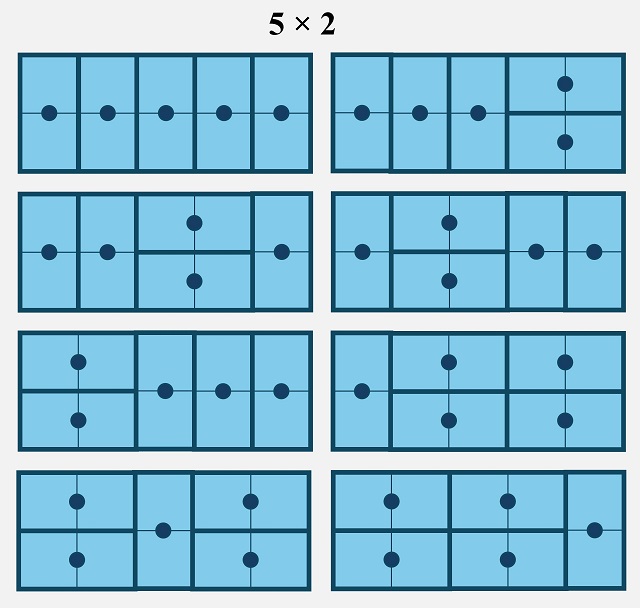
Podéis continuar con 6, 7, 8, … filas y, como se observa, se van obteniendo los números de la sucesión de Fibonacci, de nuevo.
¿Por qué aparece la sucesión de Fibonacci? La respuesta es muy sencilla. Simplemente porque es un problema cuya solución tiene la misma propiedad recursiva que la sucesión de Fibonacci y los dos primeros términos son 1 y 2. Esto es así porque para conocer los embaldosados con fichas de dominó de una cuadrícula rectangular n x 2, basta con tomar los embaldosados de la cuadrícula (n – 1) x 2 y añadirles una ficha de dominó vertical, y los embaldosados de la cuadrícula (n – 2) x 2 y añadirles dos fichas de dominó horizontales.
Veamos un ejemplo. Miremos a los embaldosados de la cuadrícula rectangular 5 x 2, que como acabamos de ver son 8. En la siguiente imagen, he tomado esos ocho embaldosados de la cuadrícula 5 x 2, he coloreado de morado los embaldosados de la cuadrícula 4 x 2, a los que se les añade una ficha de dominó vertical y he coloreado de verde los embaldosados de la cuadrícula 4 x 2, a los que se les añaden dos fichas de dominó horizontales.
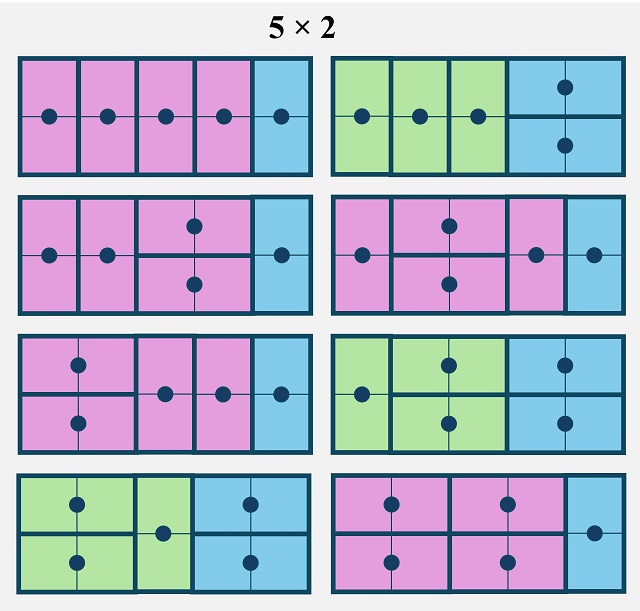
Algo similar ocurre con la cantidad de caminos posibles que recorre la abeja en su paseo hexagonal, como podéis observar.
En mi siguiente entrada de la sección Matemoción del Cuaderno de Cultura Científica volveré con más curiosos e inesperados ejemplos de apariciones de la sucesión de Fibonacci.

Bibliografía
1.- Alfred S. Posamentier, Ingmar Lehmann, The Fabulous Fibonacci Numbers, Prometheus Books, 2007.
2.- Thomas Koshy, Fibonacci and Lucas Numbers with Applications, John Wiley & Sons, 2001.
3.- Martin Gardner, Circo matemático, Alianza editorial, 1988.
4.- Fredric T. Howard, The Fibonacci Association, Math Horizons, vol. 12, n. 3,
pp. 31, 2005.
5.- Fred Whitford; Christian H Krupke, Cindy Gerber, Greg Hunt, John L. Obermeyer, Krispn Given, Max Feken, Reed Johnson, Thomas Steeger, The Complex Life of the Honey Bee: Environmental, Biological, and Chemical Challenges to Colony Health, Purdue University, 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Angel Carmel Marczuk
Excelente información para completar Teoría d Números.