Existen sucesiones de números naturales (o enteros) realmente curiosas e interesantes, no en vano, les hemos dedicado varias entradas en la sección Matemoción del Cuaderno de Cultura Científica. Entre las sucesiones de números de las que hemos hablado están la famosa sucesión de Fibonacci (véanse las entradas ¡Póngame media docena de fibonaccis!, Los números (y los inversos) de Fibonacci, ¡Nos encanta Fibonacci!, o El origen poético de los números de Fibonacci, entre otras), la musical sucesión de las vacas de Narayana (de la que hablamos en la entrada Las vacas de Narayana, la versión hindú de los conejos de Fibonacci), la sucesión de Kolakoski (sobre la que podéis leer en La misteriosa sucesión de Kolakoski), la sucesión de Levine (véase la entrada La sucesión de Levine), los números narcisistas (sobre los que puede leerse en la entrada ¿Pueden los números enamorarse de su propia imagen?), los números de Bell relacionados con la poesía (véase la entrada ¿Cuántas estructuras rítmicas existen en poesía?) o las sucesiones fractales (a la cuales hemos dedicado las entradas Sucesiones fractales, La sucesión fractal de Thue-Morse y la partida infinita de ajedrez y Sucesiones fractales: del número a la nota musical), entre otras. Por otra parte, en esta entrada hablaremos de otra interesante sucesión de números naturales, que pertenece a la familia de sucesiones de números generadas mediante “cribas”.

¿Cómo se criban los números?

En una entrada anterior ya hemos hablado de una criba famosa, la conocida criba de Eratóstenes, que sirve para obtener los números primos al ir eliminando (cribando) los números que son múltiplos de los números primos que se van obteniendo en el proceso, empezando por los múltiplos de los primeros primos 2, 3, 5 y 7, y siguiendo con los que van surgiendo en el cribado, 11, 13, 17, 19 y así todo lo que deseemos. Sobre esta criba podéis leer en las entradas Buscando lagunas de números no primos y El poema de los números primos.

Pero vayamos con la definición de la sucesión de los números de la suerte, definidos a través de una criba diferente, que no tiene en cuenta la divisibilidad, sino la posición de los números en la lista de todos los números naturales. Para ilustrarlo mejor vamos a tomar la lista de los primeros 200 números naturales y realizaremos el proceso sobre ellos.

El primer número, después de la unidad, es el número 2. Por lo tanto, vamos a eliminar uno de cada dos números de toda la lista de números naturales (imagen anterior), es decir, vamos a eliminar los números pares. Luego, después de este primer cribado, los granos (números) que caen por los agujeros de la criba son los números pares, mientras que los que permanecen en la criba son los impares.

El siguiente número, que ha quedado en la criba, es el número 3. Por lo tanto, vamos a eliminar uno de cada tres números, de los que han quedado. Empecemos, 1, 3 y eliminamos el 5, seguimos, 7, 9, y eliminamos el 11, después, 13, 15 y fuera el 17, y así se continúa como aparece en la siguiente imagen, en la cual vemos aquellos granos (números) que no han caído por los agujeros de la criba (no son el tercer número de cada triple de números consecutivos).

El siguiente número, que ha quedado en la criba, es el número 7. Por lo tanto, vamos a eliminar uno de cada siete números, de los que aún permanecen en la ficticia criba. Si miramos la imagen de arriba y vamos contando, tenemos 1, 3, 7, 9, 13, 15 y después, 19, que es el número que eliminamos, después 21, 25, 27, 31, 33, 37 y se elimina el 39, y así se continúa, de siete en siete. Al final, después de este cribado, quedan los números que aparecen en la siguiente imagen.

El siguiente número que queda en la criba, después del 7 que hemos considerado antes (por ahora tenemos en nuestra familia especial de números no cribados, luego los números de la suerte, 1, 3 y 7), es el 9, luego eliminaremos uno de cada 9 números. Por lo tanto, vamos a contar, 1, 3, 7, 9, 13, 15, 21, 25 y eliminamos el siguiente, que es 27, y así con el resto de números que vemos en la imagen anterior. El resultado de este cribado, de los números que aparecen cada nueve posiciones, está recogido en la siguiente imagen.

Lo mismo haremos con el siguiente, que es el número 13.

Tenemos 1, 3, 7, 9, 13 y 15, luego eliminaremos uno de cada 15 números, de entre los que han quedado sin cribar hasta ahora. Después llega el 21 y lo mismo, así como 25, 31, 33 y 37, quedando los números que aparecen en la siguiente imagen. Como el siguiente número es el 43, pero en el conjunto de los números que quedan sin cribar (hasta el número 200) solo quedan 39 números, ya no es posible cribar más y habremos obtenido todos los números de la suerte hasta el 200.

Por lo tanto, los números de la suerte menores que 200 son:

1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99, 105, 111, 115, 127, 129, 133, 135, 141, 151, 159, 163, 169, 171, 189, 193 y 195.

Los números de la suerte son la sucesión A000959 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS.

Estos números fueron bautizados como “números de la suerte” en el artículo On Certain Sequences of Integers Defined by Sieves / Sobre ciertas sucesiones de números enteros definidas mediante cribas, publicado por los matemáticos Verna Gardiner, R. Lazarus, N. Metropolis y S. Ulam, en la revista Mathematics Magazine (del año 1956). Más aún, los autores sugirieron el nombre de criba de Josephus Flavius para el proceso de cribado que da lugar a los números de la suerte, puesto que el proceso es similar al descrito en el conocido problema de Josefo (del que ya hablaremos en alguna otra ocasión).

Se parecen a los números primos

Los números de la suerte menores que el número 200 son 39, como acabamos de calcular, mientras que los números primos menores que 200, como habíamos calculado en la entrada El poema de los números primos [https://culturacientifica.com/2019/05/01/el-poema-de-los-numeros-primos/], son 46. En el artículo On Certain Sequences of Integers Defined by Sieves / Sobre ciertas sucesiones de números enteros definidas mediante cribas, sus autores, Verna Gardiner, R. Lazarus, N. Metropolis y S. Ulam, observaron que los números de la suerte se comportaban de forma similar a los números primos en algunas cuestiones. En particular, observaron que la frecuencia de números de la suerte entre 1 y n, para valores cada vez mayores de n, era similar a la de los números primos. En la siguiente imagen, del artículo On Certain Sequences of Integers Defined by Sieves, se recoge la tabla de números de la suerte y primos hasta el 48.600, en intervalos de 2.000 números.

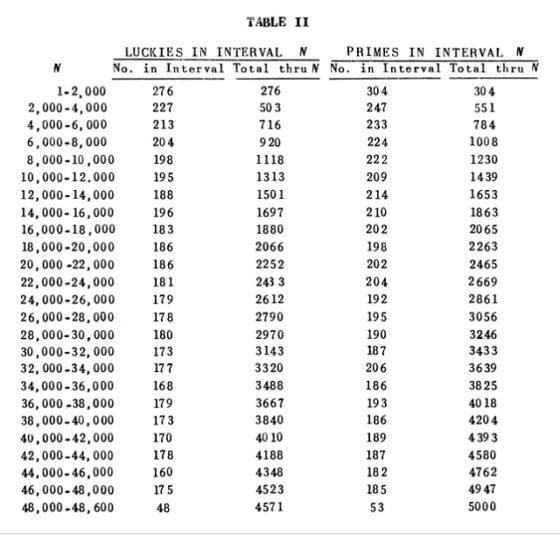
Lo que Gardiner, Lazarus, Metropolis y Ulam sugerían era que el comportamiento asintótico de los números de la suerte es similar al de los números primos, el conocido como teorema de los números primos. Este, de forma simplificada, nos dice que la función “contador de números primos”, esto es, pi(n) = cantidad de números primos menores que n, se aproxima a la función n / ln (n) -donde ln(n) es el logaritmo neperiano de n-. Este resultado fue conjeturado por el gran matemático alemán Carl Friedrich Gauss (1777-1855), con tan solo 15 años, y probado, de forma independiente, por los matemáticos franceses Jacques Hadamard (1865-1963) y Charles de la Vallée-Poussin (1866-1962).

Un año después de la publicación del artículo de Gardiner, Lazarus, Metropolis y Ulam, los matemáticos D. Hawkins and W. E. Briggs demostraron que existía un resultado análogo para los números de la suerte, es decir, que la cantidad de números de la suerte menores que n, la función s(n), se aproxima a la función n / ln (n).

Gardiner, Lazarus, Metropolis y Ulam también conjeturaron la existencia de un resultado análogo a la conjetura de Goldbach para los números de la suerte. La conocida conjetura de Goldbach (sobre la que podéis leer más en la entrada La conjetura de Goldbach) nos dice que

“todo número par mayor que dos puede escribirse como suma de dos números primos”.

Si empezamos por el principio, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 3 + 7 = 5 + 5, 12 = 5 + 7, 14 = 3 + 11 = 7 + 7, 16 = 3 + 13 = 5 + 11, … y así se continua. La conjetura de Goldbach sigue siendo una conjetura, no ha podido ser demostrada -lo que la convertiría en teorema-, a pesar de los esfuerzos realizados en ese sentido. Se sabe que se verifica para todos los pares menores que 4.000.000.000.000.000.000, pero aún no para la totalidad de los números pares.

En el artículo On Certain Sequences of Integers Defined by Sieves se conjeturó la existencia de un resultado similar a la conjetura de Goldbach para números de la suerte. En particular se probó que

“todo entero entre 1 y 100.000 puede escribirse como la suma de dos números de la suerte”.

Otro punto de conexión parece haberse establecido con los números primos gemelos. Recordemos que, como todos los números pares, a excepción del 2, son números compuestos, no primos, entonces lo más cerca que pueden estar dos números primos, salvo el 2 y el 3 que están pegados, es con solo un número par entre ellos. Y precisamente, a las parejas de números primos que están tan cerca, se les llama números primos gemelos (para más información puede verse la entrada Números primos gemelos, parientes y sexis (1)), como las parejas 11 y 13, 17 y 19, o 59 y 61.

De forma análoga, recordemos que los números pares no son números de la suerte (en este caso, ni siquiera el 2), se pueden definir los números de la suerte gemelos, como las parejas 7 y 9, 73 y 75, o 169 y 171. El gran divulgador de las matemáticas estadounidense Martin Gardner (1914-2010), en su artículo Lucky numbers and 2187 / Los números de la suerte y el 2187, afirmaba que “la cantidad de parejas de números de la suerte gemelos es igual a la cantidad de parejas de números primos gemelos”. A continuación, incluimos las parejas de números primos, respectivamente, números de la suerte, gemelos menores que 1.000.

Parejas de números primos gemelos menores que 1.000, que son 35:

(3, 5) (5, 7) (11, 13) (17, 19) (29, 31) (41, 43) (59, 61) (71, 73), (101, 103) (107, 109) (137, 139) (149, 151) (179, 181) (191, 193) (197, 199) (227, 229) (239, 241) (269, 271) (281, 283) (311, 313) (347, 349) (419, 421) (431, 433) (461, 463), (521, 523) (569, 571) (599, 601) (617, 619) (641, 643) (659, 661) (809, 811) (821, 823) (827, 829) (857, 859) (881, 883)

Parejas de números de la suerte gemelos menores que 1.000, que son 33:

(1, 3), (7, 9), (13, 15), (31, 33), (49, 51), (67, 69), (73, 75), (127, 129), (133, 135), (169, 171), (193, 195), (235, 237), (259, 261), (283, 285), (319, 321), (391, 393), (427, 429), (475, 477), (487, 489), (517, 519), (535, 537), (577, 579), (613, 615), (619, 621), (643, 645), (727, 729), (739, 741), (883, 885), (895, 897), (925, 927), (931, 933), (979, 981), (991, 993).

Y, como no podía ser de otra manera, el siguiente tema de interés ha sido el estudio de los números primos de la suerte, pero ese es otro tema del que quizás hablemos en el futuro.

Homenaje a Martin Gardner

Vamos a terminar esta entrada con un número de la suerte especial, el número 2.187, que era el número de la casa en la que vivía el divulgador de las matemáticas Martin Gardner en su niñez, en Tulsa (Oklahoma, Estados Unidos). En su artículo Lucky numbers and 2187 / Los números de la suerte y el 2187, Martin Gardner habla de las curiosas propiedades de este número de la suerte. Como afirma el Dr. Matrix (alter ego de Martin Gardner en sus artículos), “todos los números tienen infinitas propiedades inusuales”, veamos algunas del número 2.187.

A. El número 2.187 es igual a 3 elevado a la 7 (es decir, 3⁷), luego si escribimos este número en base 3, se representará como 10.000.000 (en base 3).

B. Si intercambiamos la posición de los dos últimos dígitos del 2.187 se obtiene 2.178, que multiplicado por 4 nos da 8.712, que es el número anterior (2.178) cambiado de orden (de atrás hacia delante). Más aún, si restamos 2.187 a 9.999 se obtiene 7.812, que es el mismo número, pero cambiado el orden. Seguimos con los dígitos del número 2.187, que son 2, 1, 8 y 7, y formamos los números 21 y 87, que multiplicados nos da 1.827, un número con los mismos dígitos, pero permutados.

C. Vamos a terminar con una curiosa torre de sumas que aparece al sumarle al número 2.187 números formados por las cifras básicas, empezando por el 1, en orden creciente, desde 1.234 hasta 123.456.789.

2.187 + 1.234 = 3.421

2.187 + 12.345 = 14.532

2.187 + 123.456 = 125.643

2.187 + 1.234.567 = 1.236.754

2.187 + 12.345.678 = 12.347.865

2.187 + 123.456.789 = 123.458.976

Como puede observarse, al sumar esos números con las cifras básicas en orden creciente se obtiene un número con los mismos dígitos que el número que se ha sumado al 2187, pero permutado el orden.

Bibliografía

1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – ICMAT – FESPM, 2021.

2.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.

3.- Verna Gardiner, R. Lazarus, N. Metropolis and S. Ulam, On Certain Sequences of Integers Defined by Sieves, Mathematics Magazine, Vol. 29, No. 3, pp. 117-122, 1956.

4.- D. Hawkins and W. E. Briggs, The Lucky Number Theorem, Mathematics Magazine, Vol. 31, No. 2, pp. 81-84, 1957.

5.- Martin Gardner, Lucky numbers and 2187, Mathematical Intelligencer, Vol. 19, n. 2, pp. 26-29, 1997.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica