Campo magnético y cargas en movimiento
Las interacciones entre corrientes e imanes y entre corrientes entre sí que hemos visto se entienden mucho mejor y se simplifican si se emplea el concepto de campo magnético. Si bien la partcipación de vectores parece complicar un tanto el asunto, veremos que en realidad podemos abordarlo de forma muy sencilla.

Tal y como resume la ley de Coulomb los cuerpos cargados electricamente ejercen fuerzas unos sobre otros. Cuando los cuerpos cargados están en reposo, las fuerzas son “eléctricas”, o fuerzas de Coulomb. Los “campos eléctricos” actúan como fuentes de estas fuerzas. Pero cuando los cuerpos cargados están en movimiento (como en el caso de dos cables paralelos por los que pasa corriente), existen fuerzas adicionales a las fuerzas eléctricas. Estas nuevas fuerzas son “magnéticas” y están causadas por “campos magnéticos” creados por las cargas en movimiento.
La interacción magnética de cuerpos cargados en movimiento no es tan simple como la interacción eléctrica. Como comprobó Oersted, la direccion de la fuerza eljercida por un campo creado por una corriente sobre una aguja imantada es perpendicular tanto a la dirección de la corriente como a la linea entre la aguja y la corriente. Pero, ¿cómo se comporta una carga individual cuando se mueve libremente en un campo magnético externo? Las reglas que lo explican son suficientes para entender la base de inventos que revolucionaron la civilización occidental primero y el mundo, después.
Supongamos que tenemos un campo magnético uniforme, que simbolizaremos como B (la negrita indica que es un vector, pero eso no debe preocuparnos). ¿Cómo afecta este campo externo a un cuerpo cargado en movimiento, digamos, un electrón? Experimentalmente encontramos que la fuerza depende de:
a) la carga q del electrón
b) la velocidad v del electrón, y
c) la fuerta del campo B a través del que se mueve el electrón.
La fuerza no solo depende de la magnitud de la velocidad, sino también de su dirección, por eso v está en negrita, también es un vector. Si el desplazamiento es perpendicular al campo B, entonces encontramos una relación muy simple:
F = kqvB
Donde la fuerza F es un vector también, pero la velocidad es solo el valor de su magnitud. La k que aparece es una constante de proporcionalidad cuyo valor depende de las unidades que escojamos para F, v y B.
Experimentalmente tambien encontramos que si el electrón se mueve en paralelo con el campo, entonces el valor de la fuerza es cero. Existe pues una relación entre el ángulo que forman la dirección de la velocidad con la dirección del campo. Esto es, para las direcciones que no sean la perpendicular o la paralela el valor de la fuerza estará en el máximo de la perpendicular y el mínimo (cero) de la paralela. Por lo tanto podemos decir que la fuerza para el caso general es proporcional al componente de la velocidad que es perpendicular a la dirección del campo. Si esto lo simbolizamos como v┴ podemos escribir que, para todos los casos:
F = kqv┴B
donde k es la misma constante que antes. La dirección de la fuerza es siempre perpendicular a la dirección del campo y perpendicular a la dirección del movimiento del electrón.
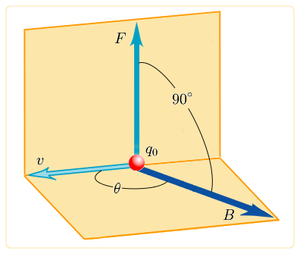
La fuerza ejercida por un campo magnético externo sobre una partícula cargada puede usarse para definir el campo magnético B de tal manera que resulte que k = 1, con lo que tenemos que:
F = qv┴B
Con esto tan sencillo estamos equipados para entender por ejemplo cómo una caída de agua puede usarse para generar una corriente eléctrica, o viceversa, cómo una corriente eléctrica puede hacer girar un motor que haga subir al agua, además de multitud de fenómenos naturales, como las auroras.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Campo magnético y cargas en movimiento |…
[…] Las interacciones entre corrientes e imanes y entre corrientes entre sí que hemos visto se entienden mucho mejor y se simplifican si se emplea el concepto de campo magnético. Si bien la partcipación de vectores parece complicar un tanto el […]
Campo magnético y cargas en movimiento |…
[…] “Las interacciones entre corrientes e imanes y entre corrientes entre sí que hemos visto se entienden mucho mejor y se simplifican si se emplea el concepto de campo magnético. Si bien la partcipación de vectores parece complicar un tanto el” […]
Hitos en la red #120 – Naukas
[…] El proyecto discreto sigue adelante: Campo magnético y cargas en movimiento […]
Trayectorias de las partículas cargadas en un campo magnético | Experientia docet | Cuaderno de Cultura Científica
[…] Viene de Campo magnético y cargas en movimiento […]
José Javier Sandonís
Comentas que cuando pones una letra en negrita haces referencia al vector. Con esa idea las ecuaciones que pones más tarde con la fuerza F y el campo magnético B en negrita (y por lo tanto vectores) no serían ciertas ya que implicarían que son vectores paralelos y no es cierto, son perpendiculares. Eso se muestra más tarde en la figura. La relación tampoco sería cierta con módulos pues, como bien dices más tarde, sólo contribuye a la fuerza la componente de la velocidad perpendicular al campo magnético B. Me temo que deberías introducir la operación de producto vectorial si quieres seguir manteniendo expresiones con vectores.
Por lo demás felicitarte por la serie de artículos. Un saludo.
Los espectros de emisión de los gases – Fluceando
[…] Los físicos sabían por la teoría de Maxwell que la luz es emitida y absorbida solo por cargas aceleradas. Esto sugería que el átomo podría contener cargas en movimiento. Podía esperarse por tanto que […]
Lucia
¿Un campo magnético constante puede poner en movimiento a un protón en reposo?
César Tomé
Si relees tu propia pregunta con cuidado y este texto, empezando por el título, la respuesta debería ser evidente.
Rodolfo
Un campo magnético variable, sí ejercerá una fuerza sobre una carga en reposo. ¿En este caso cual sería la ley que los vincula? es decir como determinar la velocidad relativa en la ecuación de Lorentz.
sporter
Con la ecuación de Maxwell rot(E)=-dB/dt. Sabiendo cómo varía B(t) podemos integrar rot(E) para obtener el campo eléctrico E generado. Luego sobre la carga en reposo q de masa m actuará una fuerza F=qE que le provocará una acceleración a=F/m. La velocidad será la integral temporal de esa acceleración.
Un nuevo estado magnético, el vortión
[…] los dispositivos y disipan energía. Controlar las memorias magnéticas con voltaje, en lugar de corrientes eléctricas, puede minimizar este gasto. Una estrategia para hacerlo podría ser el uso de los materiales […]
Foo Fighters – Fisica Cuantica y Astrofisica
[…] los campos magnéticos no modifican la trayectoria la luz pero sí la de los rayos catódicos. Sabemos que los campos magnéticos ejercen fuerzas sobre las corrientes, es decir, sobre las cargas eléctricas en movimiento. Un campo magnético desvía los rayos […]