Artistas que miran a las matemáticas
No es la primera vez que desde esta ventana matemática del Cuaderno de Cultura Científica miramos hacia el arte que se ha inspirado en las matemáticas. Obras de arte relacionadas con el teorema de Pitágoras (en la entrada Cultura pitagórica: arte), el infinito (en A infinito), la sucesión de Fibonacci (Póngame media docena de fibonaccis), los cuadrados latinos (Cuadrados latinos, matemáticas y arte abstracto), los mapas (Arte cartográfico, arte con mapas), el hipercubo y la cuarta dimensión (Hipercubo, visualizando la cuarta dimensión, parte 1 y parte 2), los números (Matemática pop o Vi el número cinco en oro), las fórmulas y expresiones matemáticas (Bernat Venet, la estética de las matemáticas) o la catenaria (Catenarias en las artes plásticas), aunque esto es solo una pequeña muestra del arte que toma la Ciencia de Pitágoras como inspiración.
En la entrada de hoy queremos centrar nuestra atención, una vez más, en aristas que se han acercado a las matemáticas, han reflexionado sobre ellas y las han incorporado a sus creaciones.
Nuestra primera artista, con una obra muy geométrica, es la italiana Luisa Sartori, que vive en Nueva York desde los años 1980. Las primeras obras que vamos a mostrar pertenecen a la exposición “Circles, triangles, and then…” (que podemos traducir como, “círculos, triángulos, y entonces…”), que tuvo lugar en la Galería A.I.R. (Artists in Residence = Artistas en residencia) de Brooklyn, Nueva York, en 2010.

En esta serie de obras Luisa Sartori investiga sobre el proceso creativo de los diseños geométricos, tan frecuentes en el arte, el diseño y la arquitectura, como son, por ejemplo, los mosaicos geométricos de la Alhambra de Granada. Trabajando con figuras geométricas básicas, círculos, triángulos o cuadrados, se construyen complejos diseños y formas geométricas.
En estas pinturas el proceso de creación del diseño geométrico es parte importante de la propia obra, por lo que no se muestra el mosaico terminado y perfecto, sino que se pueden apreciar, en lápiz, las líneas de las figuras geométricas que han participado en el proceso, como si fuese una obra que aún está sin terminar.
Más aún, algunas de las obras de la exposición, como las dos siguientes, son simplemente los procesos creativos de diseños geométricos.

En algunas de las obras, como las dos siguientes, los diseños que aparecen son embaldosados uniformes.
Los embaldosados son cubrimientos de una superficie plana mediante baldosas de unas determinadas formas. Cuando las baldosas son todas iguales y con forma de polígono regular, hablamos de embaldosados regulares. Se puede probar fácilmente (véase la explicación en la entrada Diseños geométricos de chocolate) que solamente existen 3 embaldosados regulares, los clásicos cuyas baldosas son triángulos equiláteros, cuadrados y hexágonos reglares.
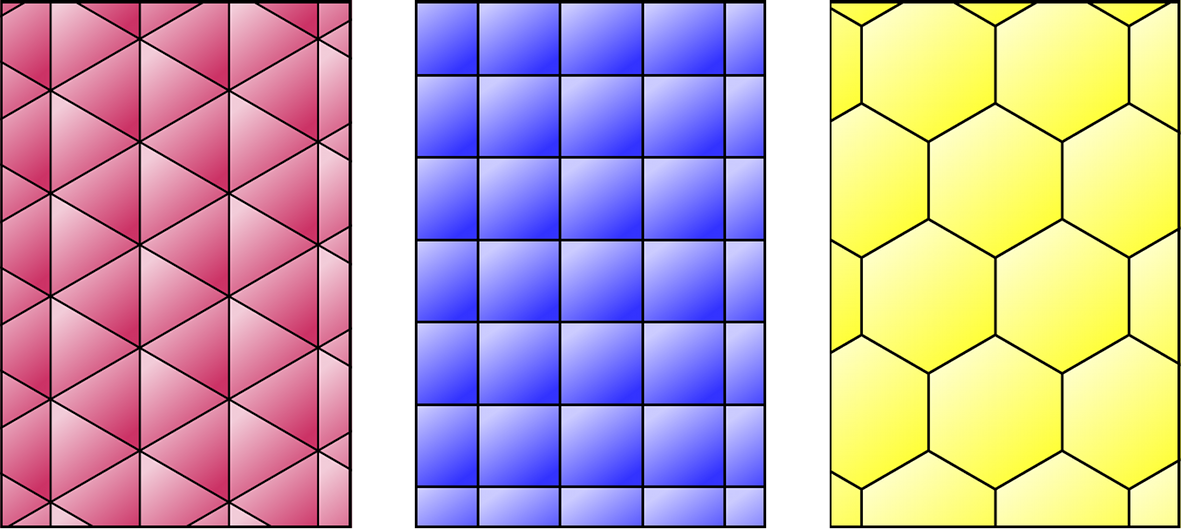
Utilizando un razonamiento similar se puede demostrar que existen 21 embaldosados uniformes diferentes, que son aquellos embaldosados en los que se puede utilizar baldosas con diferentes formas de polígonos regulares, pero con la condición de que alrededor de cada vértice del embaldosado se tiene la misma configuración de polígonos regulares. Por ejemplo, en las dos pinturas siguientes los embaldosados uniformes que aparecen son el embaldosado 4.8.8, ya que alrededor de cada vértice hay un cuadrado, un octógono y otro octógono, y el embaldosado 3.4.6.4, con un triángulo equilátero, un cuadrado, un hexágono regular y otro cuadrado, alrededor de cada vértice.

Una explicación un poco más extensa sobre los embaldosados uniformes la podéis encontrar en la guía didáctica de la exposición Imaginary, creada por el Instituto Oberwolfach (Alemania) y que ha estado en diferentes ciudades españolas de la mano de la Real Sociedad Matemática Española.
Más aún, utilizando las mismas técnicas que empleaba el artista M. C. Escher, se pueden construir nuevos embaldosados, con baldosas no regulares, pero con formas más o menos sugerentes, construidas a partir de embaldosados regulares. Esta es la técnica empleada en la obra Dhiban (2010).

Se parte de un embaldosado cuadrado, es decir, la baldosa es cuadrada, y se transforma de la siguiente forma. Lo que quitamos de un lado del cuadrado se lo añadimos en el lado contiguo, al realizar un giro de 90º, como se muestra en la siguiente imagen. Mediante reglas similares se pueden construir embaldosados muy hermosos, como los que realizaba Escher. Véase de nuevo la guía didáctica de la exposición Imaginary para conocer más sobre esta técnica.
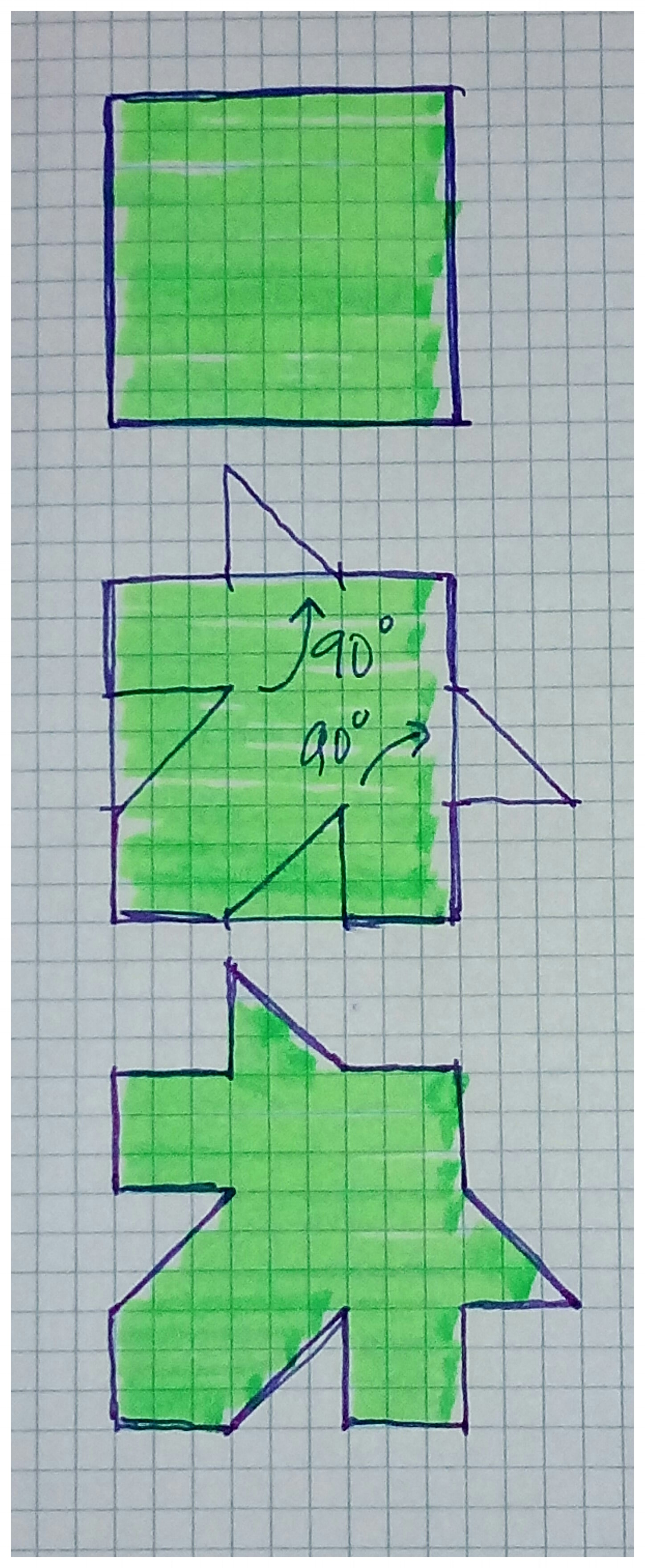
La propia Luisa Sartori realiza una obra basada únicamente en la construcción de este embaldosado.

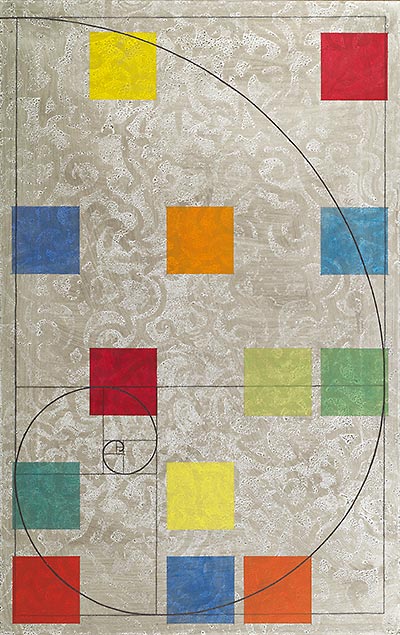
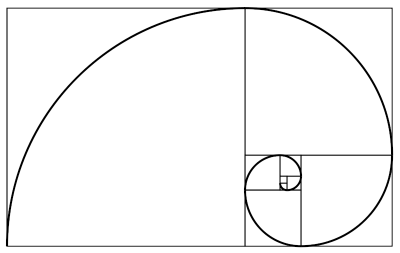
En muchas de sus obras, pertenecientes al conjunto de su producción artística, incluye diferentes elementos geométricos, aunque hoy aquí mostraremos solamente un par de ejemplos más. La primera obra, perteneciente a la serie “Here-There /High-Low” (Aquí-Allí / Alto-Bajo), incluye la conocida como espiral áurea, o de Durero, que se construye formando trozos de circunferencia a partir de una sucesión de rectángulos áureos (como se mostró en la entrada Visitad los museos, también en clave matemática).
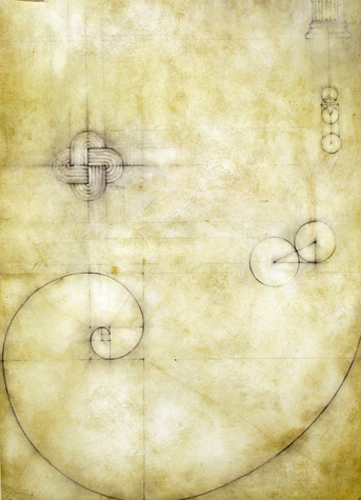
O en la siguiente obra que encontramos uno de los poliedros de da Vinci (la esfera de 72 caras), el cubo de Metatron (formado por círculos, uno central, rodeado de otros seis, creando una estructura hexagonal, y luego otros círculos alrededor) y la imagen plana de la curva loxodrómica o de rumbo constante.

Otra exposición muy interesante, desde la perspectiva de la geometría, de Luisa Sartori es su exposición de 2005, Around the center –alrededor del centro-, en la cual el círculo es un elemento principal.
Nuestra siguiente artista es la estadounidense Laura Battle. Entre sus complejas obras geométricas destacan una serie de obras que recuerdan a los hiloramas, es decir, a los diseños artísticos realizados con una serie de hilos de colores que van uniendo diferentes clavos distribuidos formando geométricas. Esta solía ser una actividad plástica muy frecuente en la educación.

A continuación, observamos una de las obras de Laura Battle que nos recuerda a un complejo hilorama.

Otra obra con diseños geométricos al estilo de los hiloramas y que además contiene una serie de curvas que nos recuerdan a las curvas trigonométricas es la obra “Color Drawing” (cuadro de color).

A lo largo de la historia del arte se pueden encontrar muchos diseños geométricos realizados mediante la intersección de circunferencias, desde la sencilla “vesica piscis” formada por la intersección de dos circunferencias y que está muy presente en el arte religioso, hasta el diseño llamado en la actualidad “flor de la vida”.
El diseño llamado “flor de la vida” está formado por una serie de circunferencias, en concreto 19 circunferencias, que se intersecan formando una estructura hexagonal. Este nombre es moderno y está relacionado con creencias místicas modernas, con lo que se ha dado en llamar la Geometría Sagrada y con el movimiento New Age, sin embargo, diseños similares a este ya a aparecen en el arte desde hace siglos.

Por ejemplo, nos lo encontramos en un mosaico en Éfeso, una localidad del siglo IX a.c. en la actual Turquía.

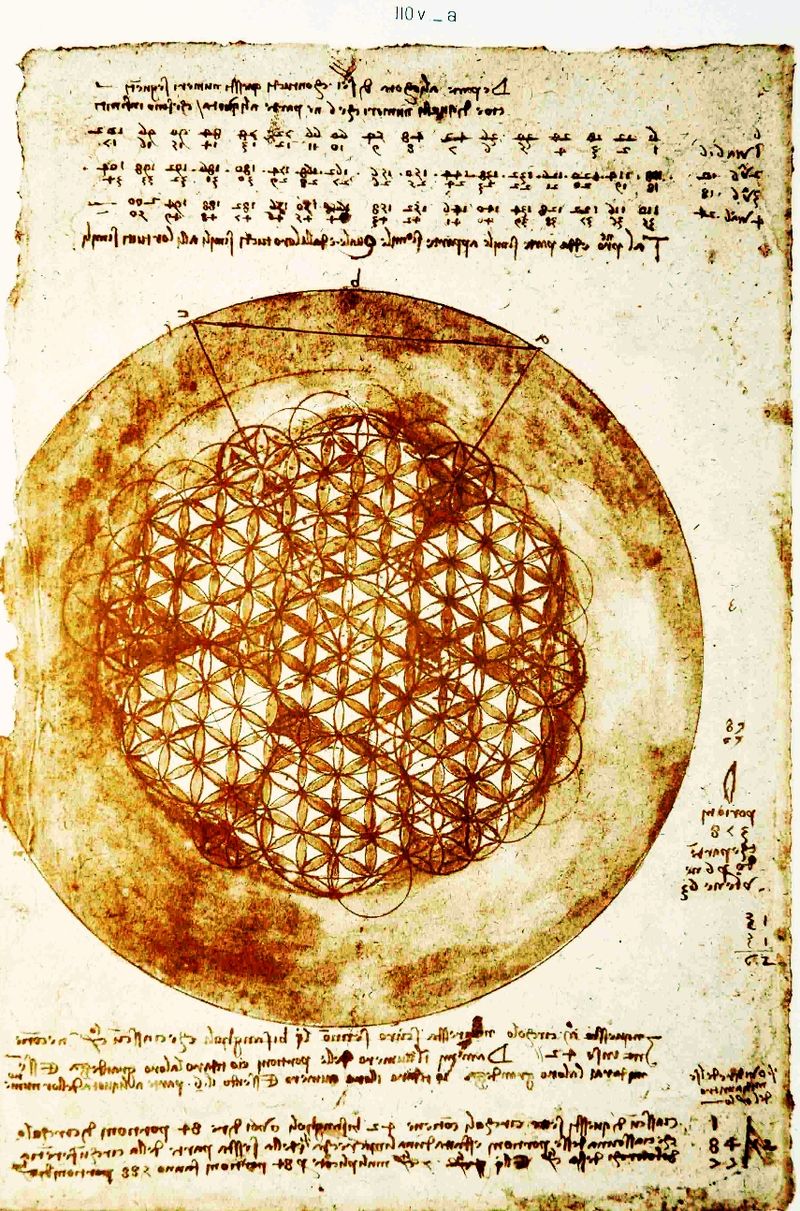
O diseños similares, como el que aparece en el Codex Atlanticus de Leonardo da Vinci.
En las obras de Laura Battle también nos encontramos estudios de intersección de circunferencias, del estilo de la “flor de la vida”, como en su obra Bloom #2, realizada a lápiz.

Sin embargo, son varias las obras de Laura Battle en las que la artista ha creado diseños geométricos mediante la intersección de circunferencias. Por ejemplo, en su obra Sin título (2006), en la que entre las formas que nos encontramos está la vésica piscis o en sus obras Roma (2004) e Incantation –Hechizo– (2010).



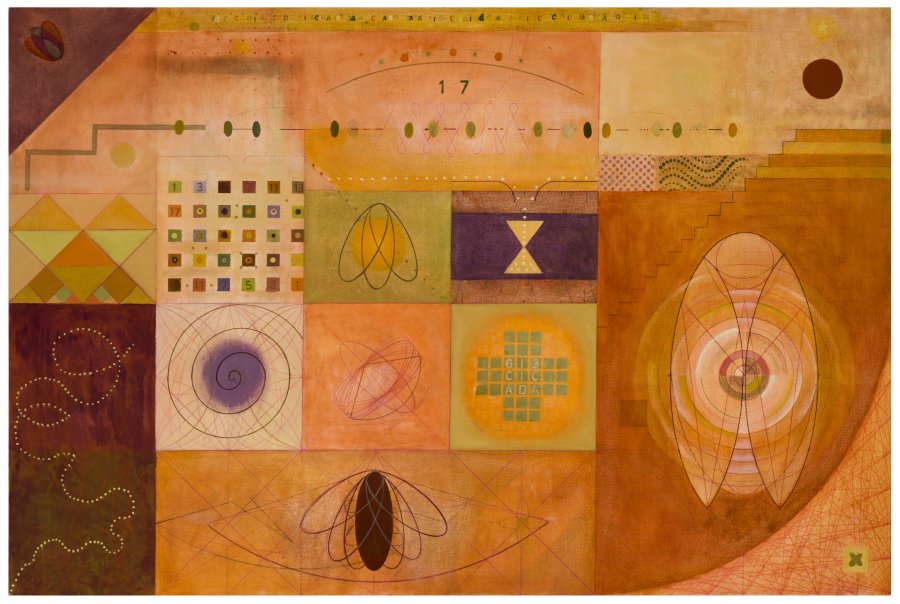
Mucho se podría decir de las obras de Laura Battle y su contenido, pero vamos a terminar con una obra más, de título Year of the cicada –el año de la cigarra– (2013), en la que encontramos elipses e intersección de las mismas, una espiral, el número primo 17, los números impares, diseños geométricos de colores o diseños de tipo fractal.
Y para terminar la entrada de hoy en la sección Matemoción del Cuaderno de Cultura Científica, una tercera artista, Cinthia Fisher, que se inspira en la ciencia, y en las matemáticas, para crear parte de sus mosaicos abstractos.
En su obra Arrangement in Black, White and Gray –Disposición en negro, blanco y gris– (2010) utiliza espirales como elemento central de su mosaico.

Se inspira en los fractales para su obra Pavement fractals -fractales de pavimiento- (2009).

Y para terminar una obra que se inspira en el clásico problema de la cuadratura del círculo. Este es un problema clásico de la matemática griega, obtener un cuadrado con la misma superficie que un círculo dado utilizando solamente la regla y el compás. En el siglo XIX se demostró que era imposible cuadrar un círculo, con únicamente la regla y el compás. Sin embargo, sí se puede cuadrar un círculo haciendo uso de la espiral de Arquímedes, que es el diseño que utiliza la artista en su obra Squaring the circle –cuadradando el círculo-.

Bibliografía
1.- Página web de Luisa Sartori
2.- Página web de Laura Battle
3.- Página web de Cinthia Fisher, Big Bang Mosaics
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
