‘Imago mundi’, 7 retratos del mundo
Hemos incluido en el título de esta entrada del Cuaderno de Cultura Científica de la UPV/EHU la expresión latina “Imago mundi”, que podríamos traducir como “imagen o representación del mundo”, porque precisamente queremos mostrar diferentes imágenes o representaciones planas del mundo en el que habitamos, el planeta Tierra.
Cuando observamos un mapamundi, un mapa del planeta, nos encontramos ante un retrato de la Tierra, sin embargo, se produce la paradoja de que no existe ninguna forma “correcta” de representar la superficie terrestre. En el año 1778, el matemático suizo Leonhard Euler (1707-1783) demostró (véase la entrada El mapa Dymaxion) que no es posible realizar mapas “correctos”, esto es, representaciones planas de la superficie terrestre dejen invariante su geometría, es decir, que preserven, salvo la escala, las propiedades métricas básicas, como las distancias entre puntos, las longitudes de curvas, los caminos más cortos (geodésicas), las áreas, los ángulos o las formas.
Como consecuencia de lo anterior, cualquier mapamundi que tomemos nos va a transmitir una imagen falsa de la superficie terrestre. Todos los mapas, sin excepción, producen distorsiones geométricas. Un estudio detallado de esta cuestión se puede consultar en cualquiera de los libros El sueño del mapa perfecto (RBA, 2010) o Portraits of the Earth (AMS, 2002).
A lo largo de la historia de la humanidad se han producido cientos de mapamundis muy interesantes, y artísticos, como puede verse en publicaciones como Mapas antiguos del mundo (EDIMAT, 1998), Joyas de la cartografía (Parragon books, 2006) o El gran libro de los mapas (Paidós, 2006). Sin embargo, el objetivo de esta entrada es mostrar una serie de diferentes retratos de la superficie terrestre, y la imagen que de ella nos transmiten, a través de diferentes representaciones (proyecciones cartográficas), relativamente modernas, de la misma.
Retrato 1: la proyección de Mercator
La proyección de Mercator es una proyección cilíndrica (una proyección basada en proyectar, mediante un proceso geométrico, la esfera terreste “básica” –con esto queremos decir que antes se reduce la esfera terrestre a escala humana- sobre una superficie cilíndrica y después desplegar esta sobre el plano), luego el mapamundi diseñado a partir de ella será rectangular; cuyos meridianos y paralelos forman una red de rectas que se cortan perpendicularmente; una proyección conforme, es decir, que preserva los ángulos, pero no las distancias, las áreas, las geodésicas (los caminos más cortos entre dos puntos) o las formas de amplios territorios; que transforma las loxodrómicas –líneas de rumbo constante- en rectas y que produce poca distorsión cerca del ecuador (que es la circunferencia de tangencia entre la esfera básica y el cilindro). Fue diseñada por el científico y cartógrafo flamenco Gerardus Mercator (1512-1594), en 1569, con el objetivo de que fuera útil para la navegación.
Como es bien conocido, la distorsión es menor cerca del ecuador y cada vez mayor según nos vamos acercando a las zonas que están más cerca de los polos. Por ejemplo, hay una distorisión muy fuerte en Groenlandia, Canada, Alaska o Rusia, que aparecen mucho más grandes de lo que realmente son. En los mapamundis con la proyección de Mercator en los que aparece Groenlandia, ésta parece de un tamaño similar a África, sin embargo, es 13 veces menor.
Aunque en Europa estamos acostumbrados a versiones en las que el meridiano de Greenwich está en el centro, existen muchas versiones centradas en otros meridianos, como la siguiente centrada en América.
O esta centrada en el océano Pacífico.
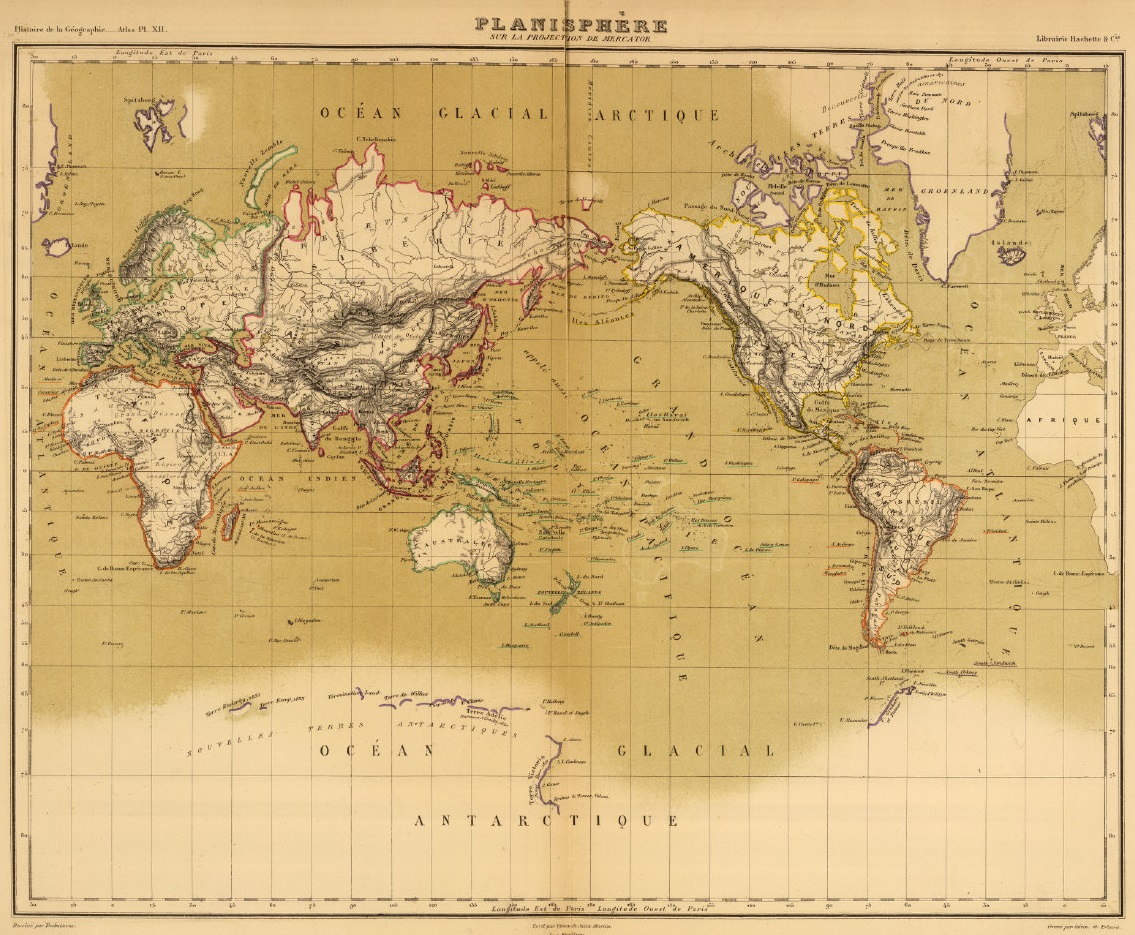
La proyección de Mercator dio lugar al diseño de mapas muy buenos para la navegación marítima y aérea, sin embargo, producía distorisiones muy fuertes en áreas y formas al alejarse del ecuador, lo que la hacía poco recomendable el uso del mapamundi generado a partir de ella. Durante mucho tiempo se sobreutilizó este mapa, pero poco a poco desde la cartografía y la geografía se empezó a demardar el uso de otro tipo de proyecciones.
Sin embargo, la proyección de Mercator ha seguido siendo muy útil en la cartografía. Por ejemplo, es la base de la proyección UTM, proyección de Mercator Transversa Universal, que se utiliza para todos los mapas de escalas menores o iguales a 1:500.000, ya que además de ser conforme, no se produce mucha distorión métrica a esa escala. Por ejemplo, el Mapa Topográfico Nacional de España, del Instituto Geográfico Nacional, que es la base de todos los mapas de España, utiliza el sistema de proyecciones UTM en sus series de mapas de escalas 1:200.000, 1:50.000 o 1:25.000 y menores, así como otras agencias similares del mundo, como la US Geological Survey, USGS.
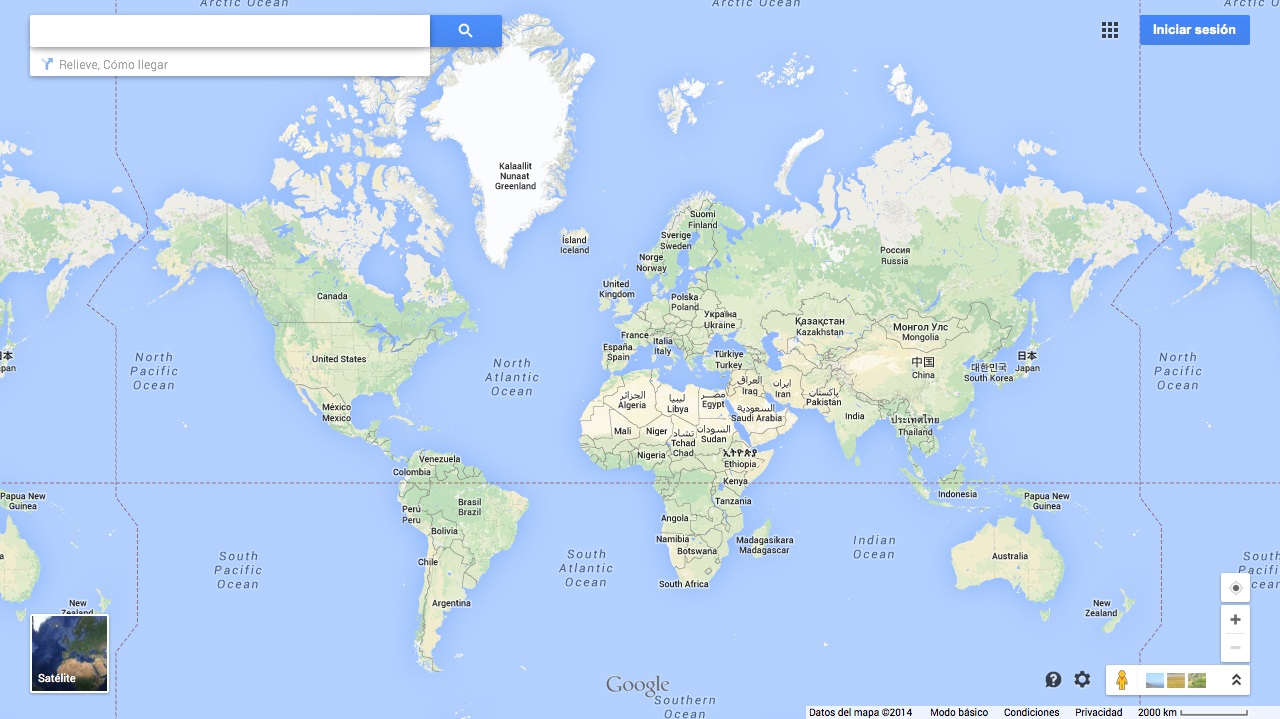
Pero uno de los usos más frecuentes hoy en día ha sido, y es, en mapas como Google Maps (donde se ha utilizado hasta este mismo año, 2018), OpenStreetMap o MapBox, entre otros, ya que es la proyección de Mercator la que está por debajo de este mapa que utilizamos practicamente todos los días en nuestra vida cotidiana. El motivo es que aunque la proyección de Mercator distorsiona mucho las formas para grandes territorios, para todo el planeta, sin embargo, el hecho de ser una proyección conforme, que preserva los ángulos, hace que distorsione muy poco las formas, localmente, para regiones pequeñas, lo cual la hace muy conveniente para un mapa dinámico sobre el que hacemos zoom a zonas pequeñas.
Retrato 2: La proyección de Mollweide
La proyección de Mollweide, también conocida con los nombres de proyección homolográfica o elíptica, fue creada por el matemático y astrónomo alemán Karl Brandan Mollweide (1774-1825) en 1805. Esta es una proyección pseudo-cilíndrica (las proyecciones cilíndricas son rectangulares y producen fuertes distorsiones en las formas, y frecuentemente en las áreas, en las zonas cercanas a los polos, por este motivo se comprimen, matemáticamente, los paralelos según se van acercando a los polos y se obtienen las proyecciones pseudocilíndricas), cuya forma es la de una elipse de proporción 2:1, es decir, el eje horizontal es el doble que el vertical; los paralelos son líneas rectas y los meridianos son semielipses, salvo el central que es una línea recta; es una proyección isoareal, esto es, que preserva el área, salvo el factor de escala, de forma que si dos regiones de la tierra tienen la misma superficie, también la tendrán en el mapa, contrariamente a lo que ocurría con la proyección de Mercator.
Si en una proyección cilíndrica se toma un meridiano como círcunferencia de tangencia, en lugar del ecuador, se tiene una versión llamada transversa de la proyección, en la cual es el meridiano el que se encuentra en la posición que antes tenía el ecuador. Si la circunferencia de tangencia es un círculo máximo (que son las geodésicas de la esfera, los caminos más cortos, y que se obtienen como intersección de la esfera con los planos que pasan por el centro de la misma), que no es ni el ecuador, ni un meridiano, se obtiene la versión oblicua de la proyección. De forma similar, se extiende la definición a las proyecciones pseudo-cilíndricas.
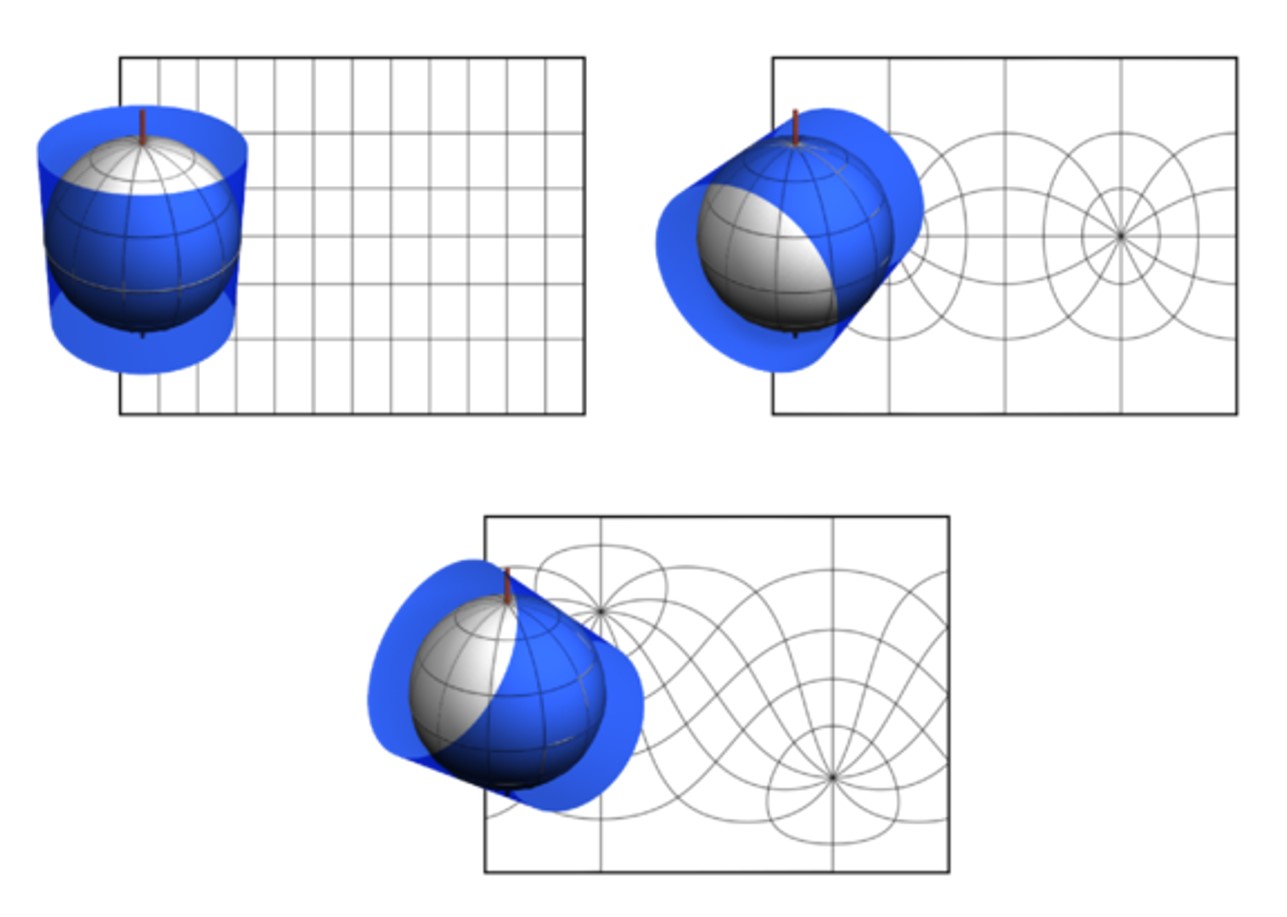
A continuación, mostramos un mapa realizado con la versión transversa de la proyección de Mollweide, con meridiano de tangencia, el meridiano de Greenwich.
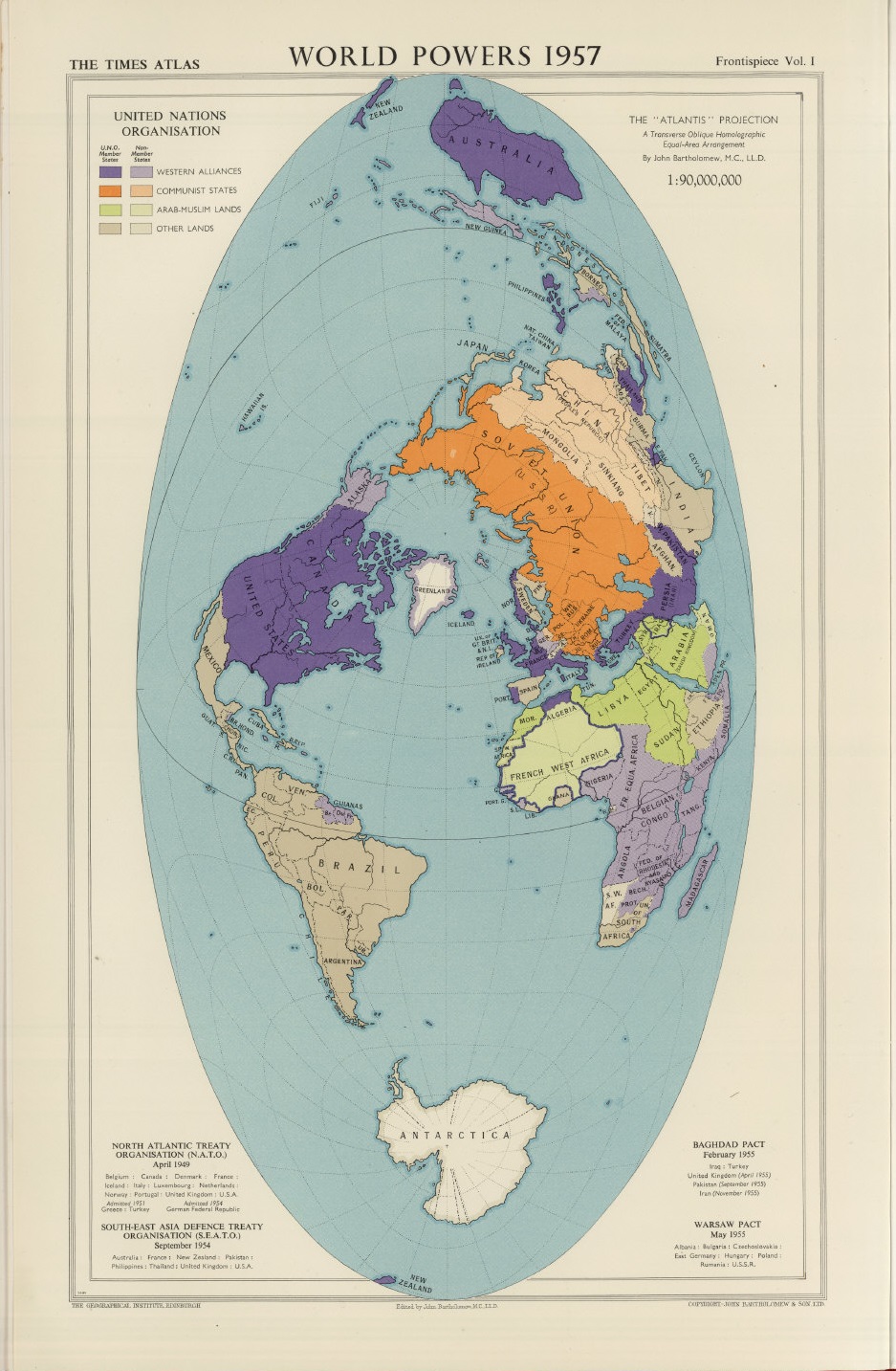
Retrato 3: La proyección de Eckert IV
En 1906 el geógrafo y cartógrafo alemán Max Eckert (1868-1938) inventó una serie de seis proyecciones pseudocilíndricas, entre ellas, la proyección Eckert IV que también es isoareal (como todas las pares de esta serie), sus paralelos son rectas y sus meridianos arcos de elipse.
Puede utilizarse, centrada en el océano Pacífico, para mostrar información sobre los océanos.
Retrato 4: La proyección de homolosena de Goode
El cartógrafo y geógrafo estadounidense Jan Paul Goode (1862-1932) estaba buscando una alternativa a la proyección de Mercator para diseñar mapas temáticos del mundo, ya que el mapa de Mercator estaba siendo sobreutilizado. En 1923 diseñó la proyección homolosena. Esta es una proyección pseudocilíndrica, como las proyecciones de Mollweide y sinusoidal en las que se basa, isoareal y su mapa está interrumpido (cortado) a lo largo de algunos meridianos.

Este mapa se hizo bastante popular y fue ampliamente utilizado en Atlas, en publicaciones científicas y divulgativas, y en medios de comunicación. En ocasiones también se la ha llamado la “proyección piel de naranja”, porque supuestamente recuerda a una naranja pelada.
También se suele mostrar este mapa interrumpido por las zonas de tierra con el objetivo de que sean precisamente las zonas oceánicas las que permanezcan despejadas.
Retrato 5: La proyección de Van der Gritten
La proyección de Van der Gritten es la que se conoce como una “proyección de compromiso o convencional”, es decir, una proyección cartográfica que no preserva ninguna de las propiedades métricas, como áreas, ángulos o geodésicas, pero intenta compensar la distorsión de todas las propiedades métricas para que ésta no sea muy grande o también para que ofrezca una imagen de la Tierra bastante creible, es decir, que mantenga bastante bien las formas globales. Por lo tanto, la proyección de Van der Gritten no preserva ni las áreas, ni los ángulos, ni las geodésicas, y por supuesto, ni las distancias, ni longitudes de las curvas. Esta proyección proyecta toda la superficie terrestre sobre un círculo, creando una fuerte distorsión en los polos, al igual que ocurría ya con la proyección de Mercator (en ocaciones se presenta recortada por los extremos).
El cartógrafo germano-americano Alphons J. van der Grinten (1852-1921) inventó esta proyección en 1898. La National Geographic Society la adoptó para el diseño de sus mapamundis en 1922, y la estuvo utilizando hasta 1988, que fue sustituida por la proyección de Robinson.
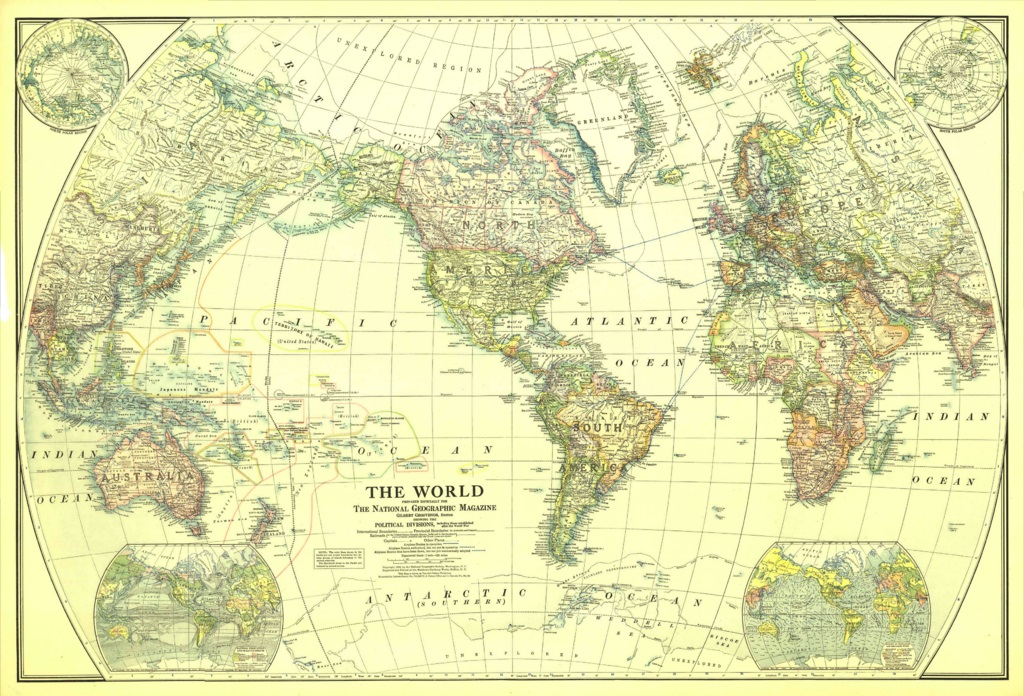
Retrato 6: La proyección central o gnomónica
La proyección central o gnomónica, considerada la proyección más antigua ya que se atribuye a Tales de Mileto (aprox. 624-547 a.n.e.), es una proyección geométrica que proyecta la esfera terrestre básica, con “rayos” que salen desde el centro de la misma, sobre un plano tangente a la esfera (por lo tanto, pertenece a la familia de proyecciones acimutales, se proyecta directamente sobre un plano, en contraposición con las cilíndricas y las cónicas).
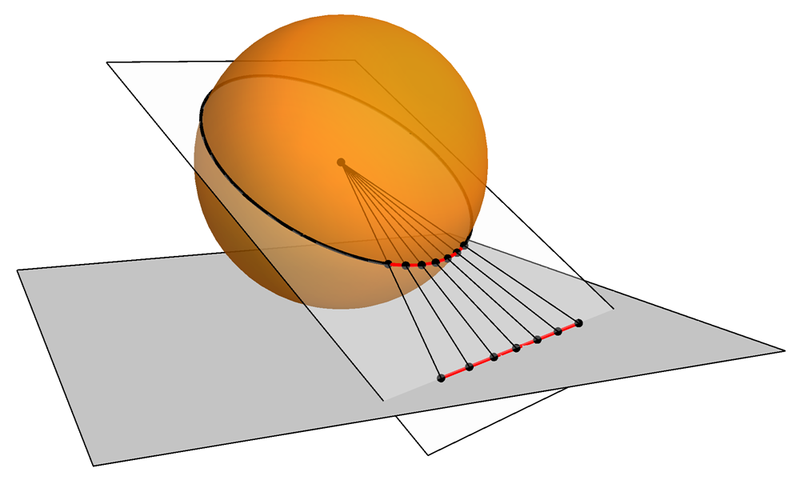
Las propiedades del mapa diseñado a partir de esta proyección son: i) su imagen es habitualmente circular y solamente cubre parte de uno de los hemisferios; ii) los círculos máximos que pasan por el punto de tangencia se transforman en rectas radiales igualmente espaciadas, mientras que los puntos que están a la misma distancia del punto de tangencia se transforman en circunferencias centradas en el punto de tangencia; iii) esta proyección preserva las geodésicas, pero no distancias, ángulos o áreas; iv) la distorsión de áreas, formas y ángulos, aunque menor cerca del centro, el punto de tangencia, es muy pronunciada según nos alejamos de dicho punto.
Por lo que acabamos de comentar, que la proyección central distorsiona mucho la imagen lejos del punto de tangencia, no es una buena proyección para diseñar directamente un mapamundi. A pesar de ello, si se ha utilizado para representar todo la superficie terrestre, a través de seis mapas conjuntos, en algunos Atlas, como en el publicado en 1844 por la Sociedad para la Difusión del Conocimiento Útil, SDUK, de Gran Bretaña.

En cualquier caso, la propiedad más importante de la proyección central es que preserva las geodésicas, es decir, los caminos más cortos, luego las rectas del plano representan los caminos más cortos de la esfera terrestre, lo cual la hace muy útil para la navegación marítima o aérea, y suele utilizarse en combinación con el mapa de Mercator, donde las rectas son las curvas de rumbo constante. Un ejemplo histótico de esta combinación es el mapa del viaje de Charles Lindberg (1902-1974), que fue el primer piloto en cruzar el oceano Atlántico solo y sin escalas, de Nueva York a París (véase el libro El sueño del mapa perfecto).
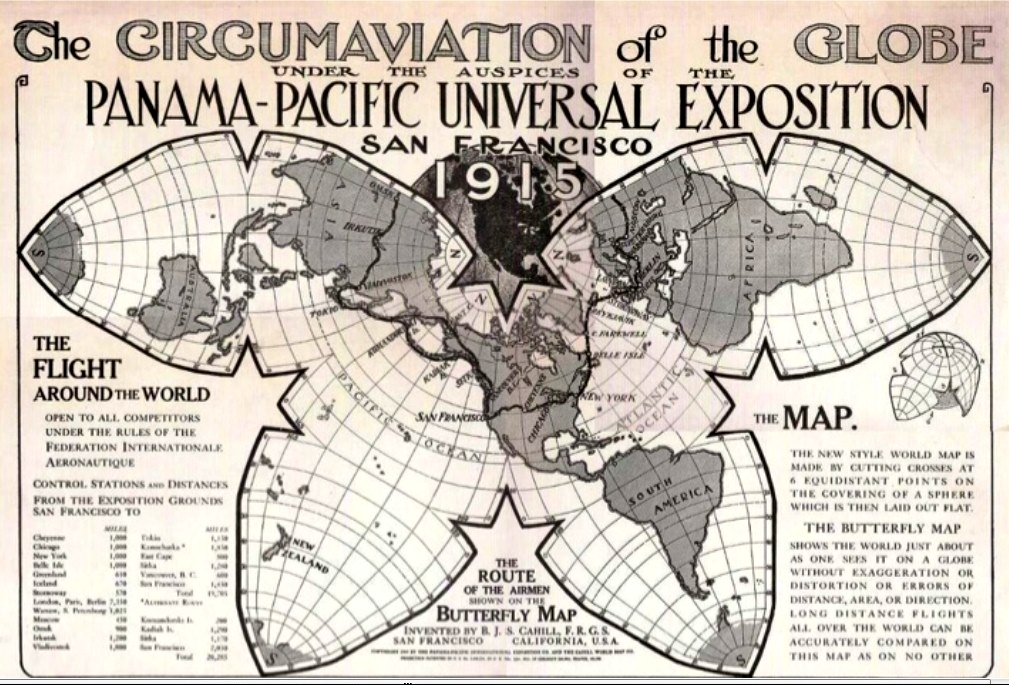
Por otra parte, además de ser utilizada para mapas celestes, la proyección gnomónica se ha utilizado para diseñar mapas poliédricos o variaciones de estos. La idea es sencilla, se circunscribe la esfera terrestre básica en un poliedro, por ejemplo, alguno de los solidos plátónicos (tetraedro, cubo, octaedro, dodecadero o icosaedro), se proyecta sobre las caras planas del mismo, y luego se despliega el poliedro en el plano.
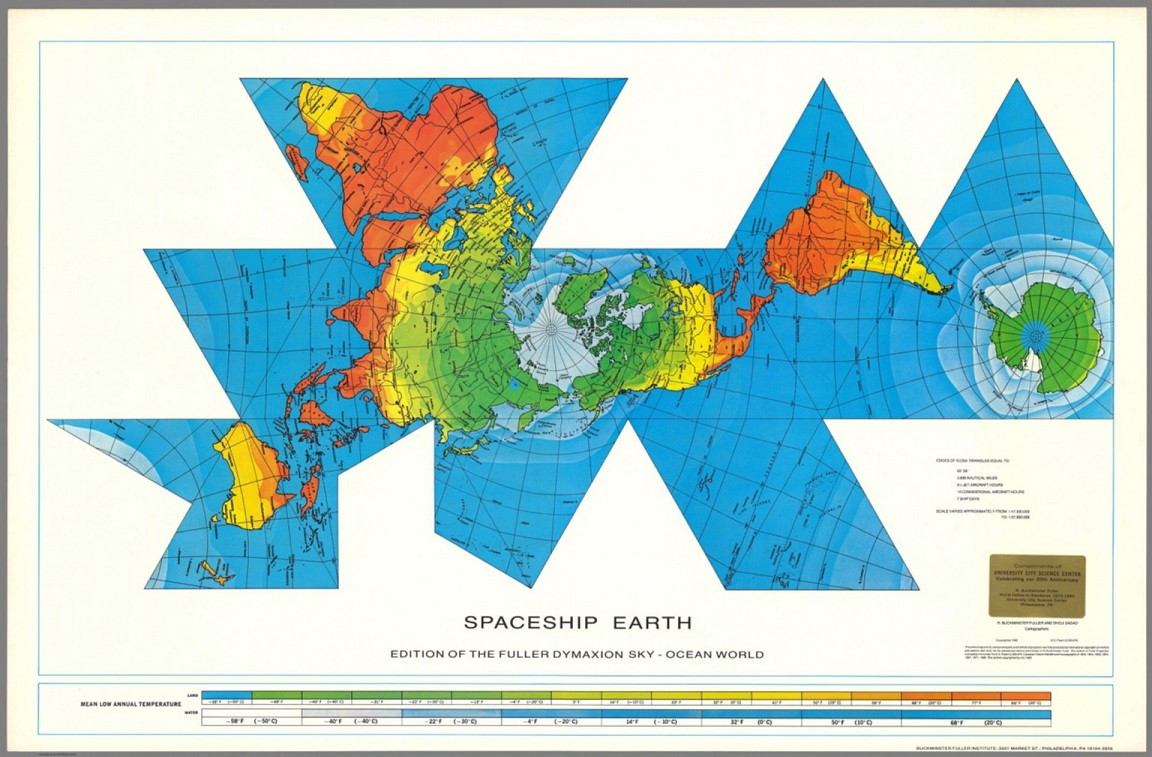
De hecho, la anterior imagen del Atlas de SDUK es un mapa cúbico, con las seis caras del cubo. Otros ejemplos son el mapa de mariposa de Cahill (1909), derivado del mapa octaédrico, o el mapa Dymaxion del diseñador y arquitecto americano Buckminster Fuller (1895-1983), que es una variación del mapa icosaédrico, del que ya hablamos en la entrada El mapa Dymaxion.
La idea de Bucky Fuller fue diseñar un mapa que no tuviera una orientación preestablecida, el eje norte-sur en la vertical y con el norte arriba, y que pudiera observarse o colocarse en cualquier dirección, cuyo centro -en la versión más habitual- estuviese en el polo norte, aunque se podían ofrecer otras visiones del mismo, que no separara o cortara los continentes, y que los mostrara juntos, formando una especie de isla rodeada por los océanos, que rompiese esa imagen (horizontal y lineal) de los mapas rectangulares, que se había ido estableciendo en las mentes de las personas llegando a distorsionar la imagen que tenían del mundo, y que además intentara crear la menor distorsión métrica posible.
Retrato 7: La proyección estereográfica
Esta proyección geométrica es también muy antigua y se suele atribuir a Hiparco de Nicea (aprox. 190-120 a.n.e.). Al igual que la proyección central, la proyección estereográfica es una proyección geométrica acimutal, pero ahora se proyecta desde un punto de la superifice terrestre básica, por ejemplo, el norte, sobre un plano tangente en el punto diametralmente opuesto, luego sería el sur (que será el centro del mapa).
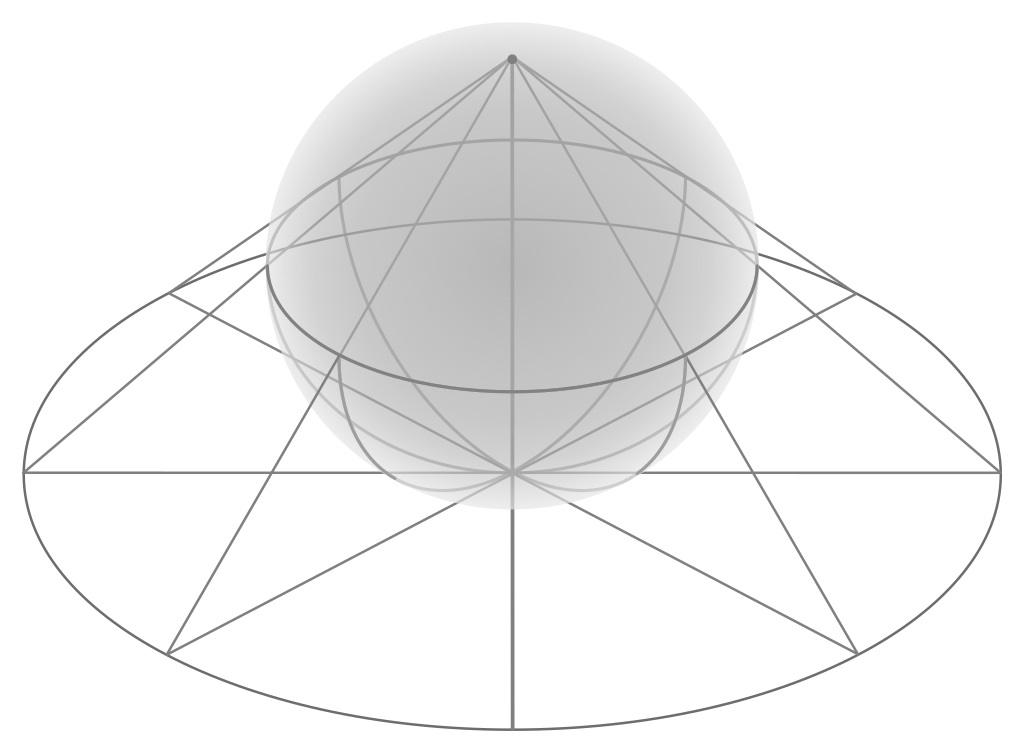
Algunas de las propiedades del mapa diseñado utilizando la proyección estereográfica son: i) su imagen se suele tomar circular, debido a que es acimutal, y cubriendo solamente uno de los hemisferios. Aunque se podría cubrir una extensión aún mayor no es recomendable por el aumento en la distorsión; ii) la proyección es conforme, es decir, preserva los ángulos, aunque no preserva ni las geodésicas, ni el área, y por supuesto tampoco las distancias; iii) al ser una proyección azimutal sí preserva las geodésicas que pasan por el punto de tangencia, es decir, para el caso en el que uno de los polos sea el foco de proyección, los meridianos se representan como rectas que pasan por el centro del mapa; iv) todos los meridianos y los paralelos, aunque más generalmente todas las circunferencias de la esfera, máximas y también normales, se proyectan en circunferencias sobre el plano, con excepción de las que pasan por el punto de tangencia, que se transforman en rectas (esta es una propiedad particular de las aplicaciones matemáticas denominadas inversiones, y la proyección estereográfica es una inversión); v) las loxodrómicas o líneas de rumbo fijo (i.e. las curvas sobre la esfera que forman un ángulo constante con los meridianos) se transforman en espirales logarítmicas.
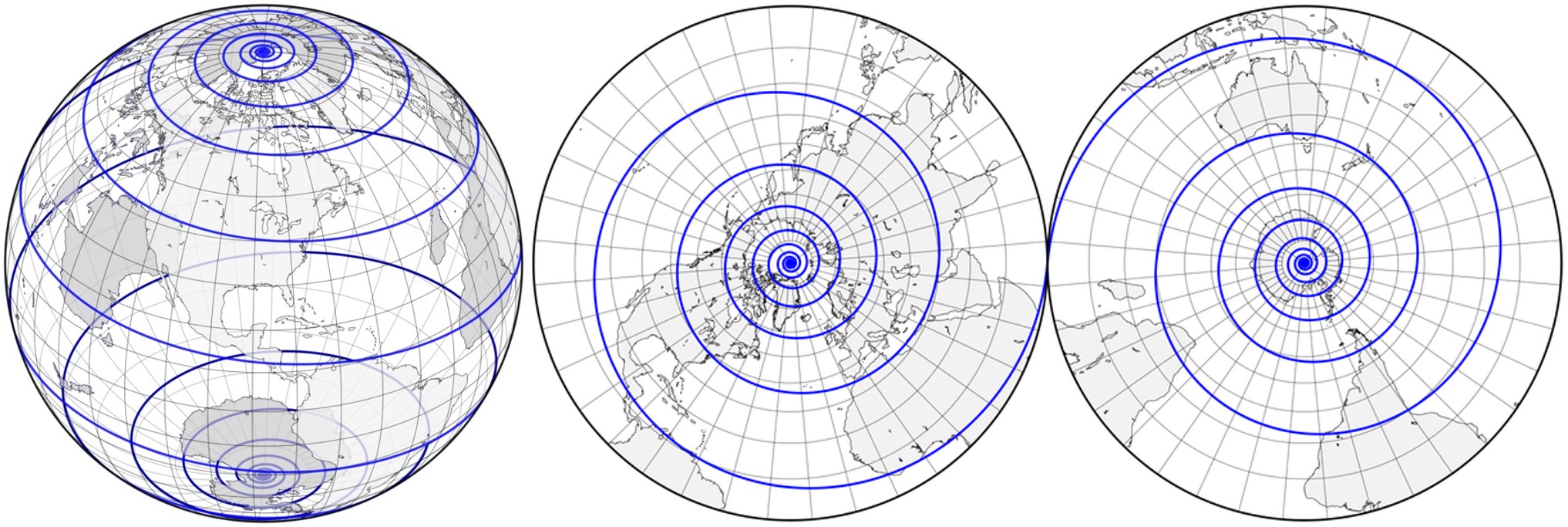
Además de para realizar mapas celestes, la proyección estereográfica fue utilizada (con el centro en algún punto del ecuador) en los siglos XVII y XVIII para diseñar mapas de dos hemisferios. Posteriormente, fueron utilizadas otras proyecciones, por ejemplo, las globulares, para los mapas en dos hemisferios.
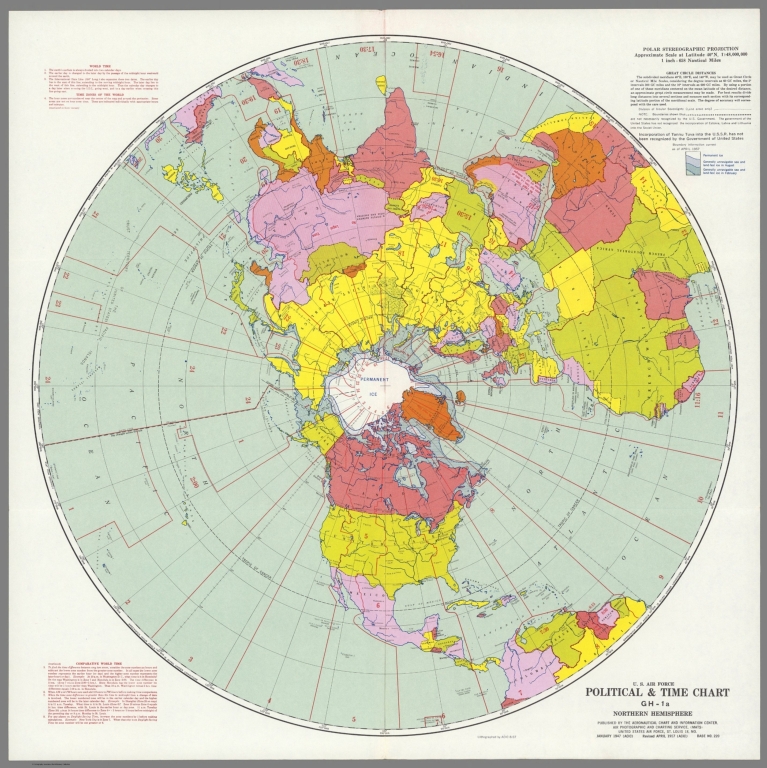
En la actualidad es muy utilizado para el diseño de los mapas polares.
Las proyecciones cartográficas también pueden utilizarse para realizar mapas de la luna u otros planetas.
En mi siguiente entrada seguiremos con algunos retratos más, realizados con proyecciones como la de Gall-Peters, Robinson, Winkel-Tripel o la acimutal equidistante, entre otras

Y más arte con mapas en la entrada Arte cartográfico. Arte con mapas
Bibliografía
1.- Raúl Ibáñez, El sueño del mapa perfecto; cartografía y matemáticas, RBA, 2010.
2.- Raúl Ibáñez, Muerte de un cartógrafo, Un paseo por la Geometría, UPV/EHU, 2002. Versión online en la sección textos-on-line de divulgamat [www.divulgamat.net
3.- Timothy G. Feeman, Portraits of the Earth; A Mathematician looks at Maps, AMS, 2002.
4.- Federico Romero, Rosa Benavides, Mapas antiguos del mundo, EDIMAT, 1998.
5.- John O. E. Clark (editor), Joyas de la cartografía, 100 ejemplos de cómo la cartografía definió, modificó y aprehendió el mundo, Parragon books, 2006.
6.- Peter Barber (compilador), El gran libro de los mapas, Paidós, 2006.
7.- David Rumsey Map Collection
8.- Centro de Mapas y Educación Norman B. Leventhal, en la Biblioteca Pública de Boston
9.- Buckminster Fuller Institute
10.- Digital Museum of Planetary Mapping
11.- Carlos Furuti, Map projections
12.- Página web del artista Juan Sukilbide
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Carmen
Me ha encantado esta explicación de las distintas formas de representación plana de la Tierra.
Hacía mucho tiempo que no lo revisaba y «me lo has puesto muy fácil».
Muchas gracias, Raúl!
Siempre es un placer leer tus entradas.
Salu2.
Carmen.
Raúl Ibáñez
Muchísimas gracias Carmen,
espero que la segunda parte te guste también.
Gracias por tus palabras.
Un abrazo, Raúl.
Angel
Al hablar del uso de la proyección UTM debería decir que se utiliza para todos los mapas de escalas 1:500000 y MAYORES. Igualmente al hablar del uso de esta proyección por el IGN para los mapas de España, debería decir 1:50000 y MAYORES.
( Un mapa a 1:50.000 es de mayor escala que uno a 1:100.000. Al igual que 1/3 de una tarta es mayor que 1/4 ?)
Raúl Ibáñez
Muchas gracias por el comentario. Sí, es cierto, la escala es «mayor».
Jose Vte. Fdez. de Sevilla Marco
Excelencia, articulo. Comparto.
Raúl Ibáñez
Muchas gracias 🙂
'Imago mundi' 2, otros 6 retratos del mundo – Cuaderno de Cultura Científica
[…] anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica, titulada Imago mundi, 7 retratos del mundo, estaba dedicada a mostrar diferentes retratos del mundo, en concreto, 7 mapas diferentes del […]
‘Imago mundi’, finalmente 9 retratos más del mundo – Cuaderno de Cultura Científica
[…] mundo, realizados con diferentes proyecciones cartográficas (matemáticas). En la primera entrega, ‘Imago mundi’, 7 retratos del mundo, las 7 proyecciones cartográficas utilizadas fueron: la proyección cilíndrica conforme de […]
El tamaño sí importa, que se lo pregunten a Colón (o de la geometría griega para medir el diámetro de la Tierra) – Cuaderno de Cultura Científica
[…] conocidos grabados de mares azules y bordes amarillos, uno de cuyos mapas puede verse en la entrada Imago mundi, 7 retratos del mundo), la obra se convierte en una referencia fundamental en geografía y cartografía, y un auténtico […]