Una de mis pasiones dentro de las matemáticas es el estudio de aquellos pequeños problemas matemáticos o de ingenio que surgieron dentro de la matemática recreativa como sencillos divertimentos matemáticos, pero que fueron creciendo con el interés de muchos matemáticos que dedicaron su tiempo a pensar sobre ellos y que se acabaron convirtiendo en hermosos diamantes, con una interesante investigación matemática a su alrededor.

Sobre algunos de estos problemas matemáticos clásicos hemos hablado en el Cuaderno de Cultura Científica, como El problema de las estudiantes de Kirkman, El problema de los sellos de Sylvester, El problema de la plantación de árboles en fila, El problema de las cartas extraviadas, El teorema de los cuatro colores, El problema de Malfatti, o , entre otros.

En esta entrada de la sección Matemoción vamos a hablar de otro de estos problemas clásicos, el conocido como problema de la cuadratura del cuadrado, del que ya hemos hablado brevemente en otras dos entradas, Blanche Descartes y la cuadratura del cuadrado y Teselaciones rítmicas perfectas.

El problema, enunciado de forma sencilla, sería el siguiente:

Problema de la cuadratura del cuadrado (o rectángulo): Dividir un cuadrado (o rectángulo) en un número finito de cuadrados más pequeños, todos de distintos tamaños.

Vayamos con algunos conceptos que vamos a utilizar a lo largo de esta entrada. La cuadratura, o disección, de un rectángulo (en particular, de un cuadrado) en cuadrados más pequeños, todos de distintas dimensiones, como se plantea en el problema, se denomina perfecta. A la cuadratura de un rectángulo que contiene la cuadratura de algún sub-rectángulo se le llama compuesta, mientras que si no existe un sub-rectángulo tal, diremos que es simple. Se llama orden de la cuadratura al número de cuadrados que se han utilizado en la cuadratura del rectángulo. La cuadratura del rectángulo de la imagen anterior es perfecta y simple.

Por otra parte, los lados de los cuadrados pequeños tienen que ser múltiplos racionales de los lados del cuadrado (o del rectángulo) grande, por lo tanto, podemos trabajar con cuadrados tales que sus lados tengan longitud entera, así como los lados del rectángulo grande.

En la página Sources in recreational mathematics, an annotated bibliography, el matemático estadounidense David Singmaster menciona que la primera persona que publica, que se tenga constancia de ello, sobre algún problema relacionado con la cuadratura del cuadrado es el matemático recreativo inglés Henry E. Dudeney (1857-1930). En su conocido libro Los acertijos de Canterbury, publicado en 1907, publica el problema El joyero de Lady Isabel, que decía lo siguiente.

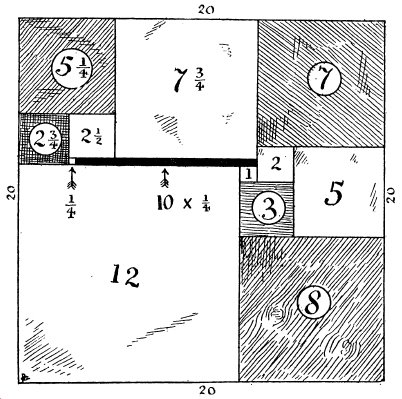
El joyero de Lady Isabel: La joven prima y pupila de Sir Hugh, Lady Isabel de Fitzarnulph, era conocida por todo el mundo como “Isabel la Bella”. Entre sus tesoros había un joyero, cuya tapa superior tenía la forma de un perfecto cuadrado. La tapa del joyero estaba incrustada con trozos de madera y una franja de oro de 10 pulgadas* de largo por un cuarto de pulgada de ancho.

Cuando los jóvenes empezaron a pedir la mano de Lady Isabel, Sir Hugh prometió que daría su consentimiento a aquel que consiguiese decirle las dimensiones de la tapa del joyero con solo los siguientes datos: que había una franja rectangular de oro de 10 pulgadas de largo por 1/4 de pulgada de ancho; y el resto de la tapa estaba incrustado exactamente con trozos de madera, cada uno de los cuales era un cuadrado perfecto y no había dos piezas del mismo tamaño. Muchos jóvenes fracasaron, pero uno de ellos finalmente tuvo éxito. El rompecabezas no es uno de los fáciles, pero las dimensiones del rectángulo de oro, junto con las otras condiciones, determinan completamente el tamaño de la tapa del joyero.

[* Recordemos que una pulgada es una medida de longitud inglesa equivalente a 25,4 milímetros]

El propio Henry Dudeney decía en la solución al problema que este no era precisamente un rompecabezas sencillo. La solución, única, era que la tapa del joyero era un cuadrado de 20 pulgadas de lado, como se muestra en la imagen.

Aunque este rompecabezas ya había sido publicado, como comenta David Singmaster, por Henry Dudeney en enero de 1902, en el número 584 de la revista The London Magazine. En cualquier caso, el problema de Dudeney no era realmente una cuadratura del cuadrado, ya que incluía un rectángulo en la disección del mismo, aunque se le aproximaba mucho y sugería un interés en el problema de la cuadratura del cuadrado.

El problema de la cuadratura del cuadrado (o del rectángulo) debía de interesar ya desde tiempo atrás, puesto que en 1903 el matemático alemán Max Dehn (1878-1952), que era estudiante del matemático alemán David Hilbert (1862-1943) y que en su habilitación de 1900 había resuelto el tercer problema de los famosos problemas del milenio del propio Hilbert, publicó el primer trabajo matemático sobre la “disección de un rectángulo en cuadrados más pequeños”. Demostró que un rectángulo podía ser diseccionado en cuadrados más pequeños si y sólo si la proporción entre su altura y su anchura era un número racional.

En la obra póstuma del jugador de ajedrez y matemático recreativo estadounidense Sam Loyd (1841-1911) Cyclopedia of 5000 Puzzles (Los acertijos de Sam Loyd), publicada en 1914, se incluía el rompecabezas de la colcha de retazos (the patch quilt puzzle), que planteaba dividir una colcha cuadrada con 13 x 13 cuadraditos pequeños en retales cuadrados de una, o más piezas. Es decir, el problema de diseccionar un cuadrado en cuadrados más pequeños, aunque sin importar que se repitan los tamaños de estos.

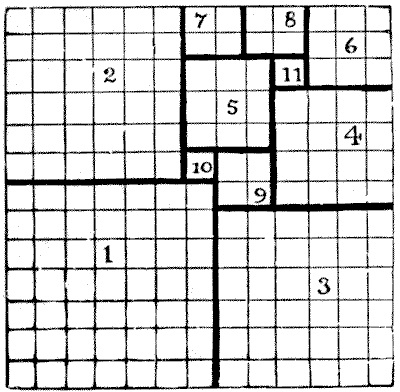
David Singmaster menciona que este rompecabezas había sido publicado previamente, en 1907, por Sam Loyd en la revista Our Puzzle Magazine. Además, también aparecería en el libro de Henry Dudeney Amusements in Mathematics (1917), con el nombre La colcha de la señora Perkins. Por este motivo el problema de diseccionar un cuadrado en cuadrados más pequeños, permitiendo que estos tengan el mismo tamaño se conoce como el problema de la colcha de la señora Perkins.

Aunque recordemos que en esta entrada estamos interesados en el problema de la cuadratura perfecta del cuadrado, es decir, la disección de un cuadrado, o rectángulo, en cuadrados más pequeños todos de distintos tamaños, y no en el problema de la colcha de la señora Perkins.

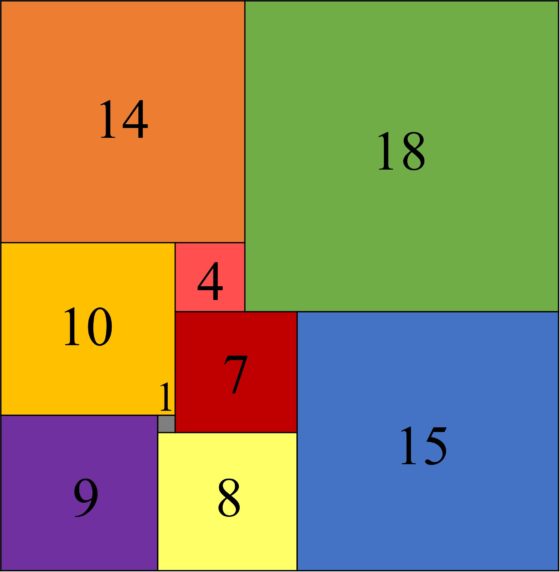
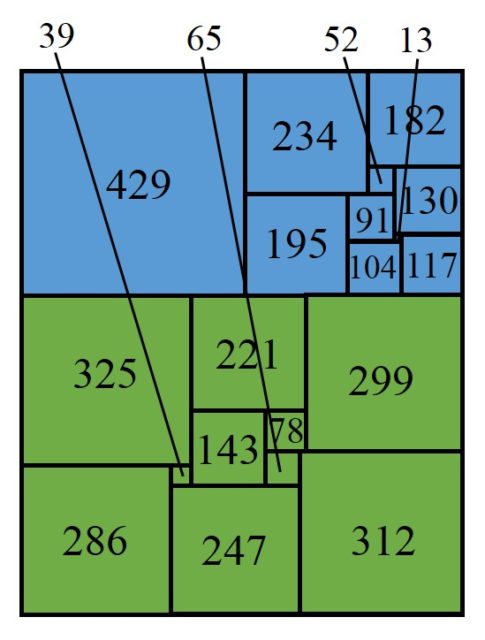
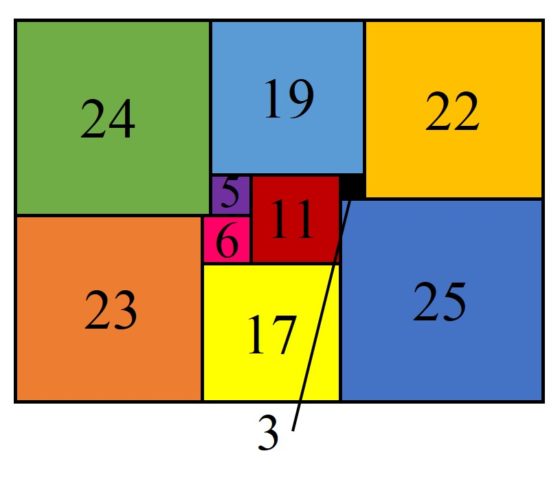
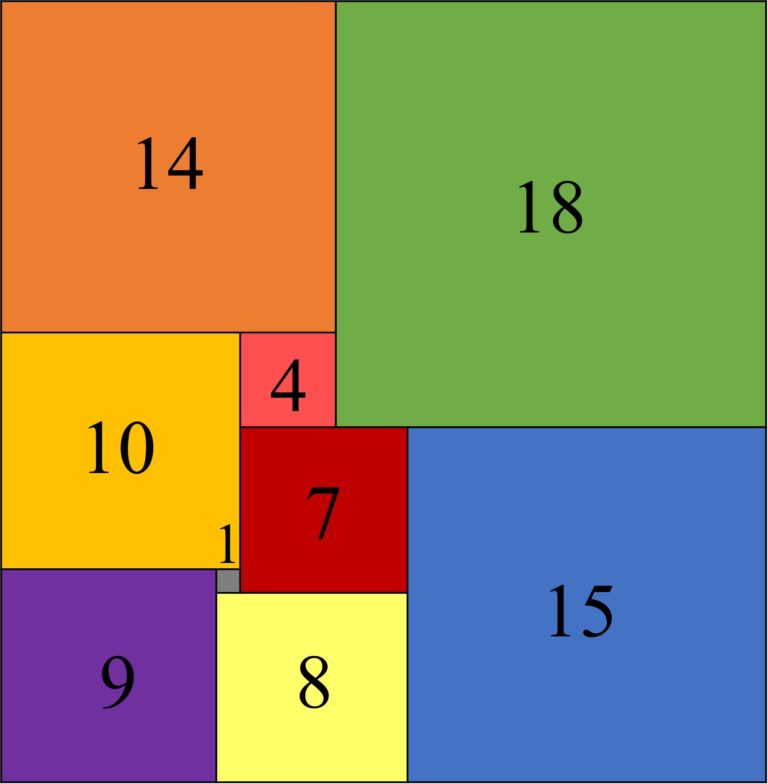
Los primeros ejemplos de rectángulos con cuadraturas perfectas y, además, simples, fueron publicados en 1925 por el matemático polaco Zbigniew Moron (1904-1974), en el artículo O Rozkladach Prostokatow Na Kwadraty (Sobre la disección de un rectángulo en cuadrados). Eran el rectángulo de tamaño 33 x 32 dividido en 9 cuadrados distintos (orden 9), cuyos lados eran 1, 4, 7, 8, 9, 10, 14, 15 y 18, que aparece en la primera imagen de esta entrada y el rectángulo de tamaño 65 x 47, dividido en 10 cuadrados distintos (orden 10), con lados 3, 5, 6, 11, 17, 19, 22, 23, 24 y 25, que mostramos a continuación.

En los años 1930 el problema de descomponer un cuadrado en un número finito de cuadrados de distintos tamaños fue añadido, por el matemático polaco Stanislaw Ruziewicz -que era quien le había hablado a Zbigniew Moron del problema de la cuadratura del rectángulo- al Cuaderno escocés, como el problema número 59. Un grupo de matemáticos polacos, conocidos como La escuela matemática de Lwow (entre los matemáticos relacionados con esta escuela estaban Stephan Banach, Marek Mac, Kazimierz Kuratowski, Stanisław Mazur, Hugo Steinhaus o Stanislaw Ulam, entre otros), se reunían en el Café Escocés de Lwow para hablar de problemas matemáticos. Solían escribir con lápiz sobre el mármol de las mesas, pero al final del día las mesas se limpiaban y se perdían los problemas y discusiones que habían tenido. Por este motivo, a partir de 1935 decidieron recoger los problemas y soluciones en un cuaderno que sería conocido como Cuaderno Escocés. El último problema, número 193, es de 1941.

Poco tiempo después, el matemático japonés Michio Abe construyó más de 600 rectángulos perfectos simples, que recogió en el artículo Covering the square by squares without overlapping (Recubriendo un cuadrado con cuadrados que no se solapan) publicado en 1930 en la revista Journal of Japan Mathematical Physics. Además, en un segundo artículo publicado en 1931 mostró la construcción de una serie infinita de rectángulos perfectos compuestos, construidos a partir de un rectángulo perfecto simple de tamaño 195 x 191.

¿Y qué ocurría con la cuadratura perfecta del cuadrado? Por un lado, sabemos que alrededor del año 1930, el gran matemático húngaro Paul Erdös (1913-1996) había conjeturado que cualquier disección de un cuadrado en cuadrados más pequeños tenía que contener, al menos, dos cuadrados del mismo tamaño, luego no podía ser perfecta. Por otra parte, existía en ese tiempo una conjetura del matemático ruso Nikolai N. Luzin (1883-1950), la conjetura de Luzin, según la cual era imposible diseccionar un cuadrado en un número finito de cuadrados distintos. El matemático belga Maurice Kraitchik (1882-1957), en su libro La mathématique des jeux ou Récréations mathématiques (1930), afirmaba que en una comunicación personal el matemático Luzin le había hablado de esa conjetura. Quizás la conjetura de Luzin llegó a oídos de Erdös o ambos conjeturaron lo mismo de forma independiente, pero lo cierto es que en los años 1930 se creía que la cuadratura (perfecta) del cuadrado era imposible.

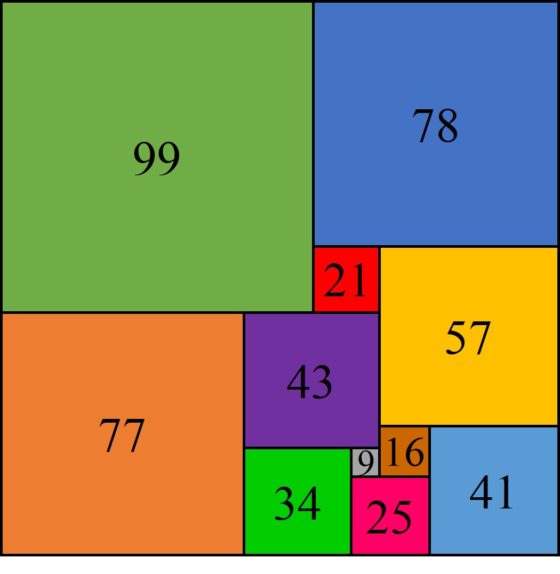
Pero la historia continúa. Como cuenta el matemático británico William Th. Tutte (1917 – 2002) en su artículo Squaring the square (Cuadrando el cuadrado), publicado por Martin Gardner en su columna de juegos matemáticos de la revista Scientific American, su colega Arthur H. Stone (1916-2000), cuando aún eran estudiantes en la Universidad de Cambridge (Gran Bretaña), quedó intrigado por la supuesta imposibilidad de descomponer un cuadrado en cuadrados más pequeños distintos, relacionada con el problema planteado por Dudeney en Los acertijos de Canterbury. Entonces intentó probar, sin éxito, dicha imposibilidad, aunque acabó construyendo una disección perfecta de un rectángulo de dimensiones casi cuadradas, 177 x 176, en 11 cuadrados más pequeños.

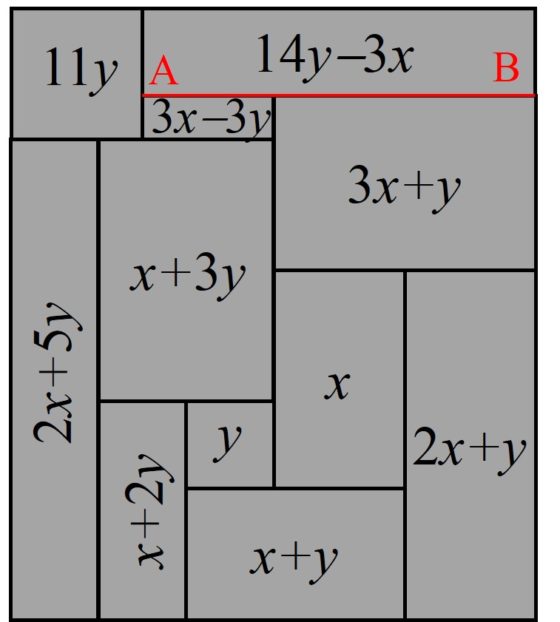
El método empleado para construir este rectángulo es sencillo. Se parte de un rectángulo que se divide en rectángulos más pequeños, por ejemplo, como aparece en la siguiente imagen que contiene 11 rectángulos. Se asume que ese diagrama nos da realmente una descomposición en cuadrados de un rectángulo, pero asumiendo que hemos dibujado mal la descomposición cuadrada del rectángulo, es decir, el rectángulo grande sí es un rectángulo, aunque quizás de dimensiones distintas a las que aparece en el dibujo, y los rectángulos pequeños son realmente cuadrados mal dibujados. Se empieza dando valor a los lados de dos de los pequeños cuadrados (en la imagen rectángulos) que estén juntos, de valores x e y, y se van calculando los valores de los lados de los demás cuadrados pequeños, en relación a estos, con sencillas expresiones algebraicas. Por ejemplo, el cuadrado debajo de los cuadrados de lados x e y, sería un cuadrado de lado x + y, el pequeño cuadrado a la derecha de los de dimensiones x y x + y tendrá lado 2 x + y, y así con el resto de cuadrados. De esta manera, todos los cuadrados encajan bien, unos con otros, salvo quizás los que están a ambos lados de la línea AB de la imagen, por lo que hay que elegir valores de x e y para que ahí también encajen, es decir, 14 y – 3 x = (3 x – 3 y) + (3 x + y). Despejando, 16 y = 9 x. Y tomando x = 16 e y = 9 se obtiene la cuadratura perfecta de un rectángulo de dimensiones 177 x 176, encontrada por Stone.

Entonces, el joven Arthur Stone y sus tres compañeros, también estudiantes del Trinity College de la Universidad de Cambridge, Rowland L. Brooks (1916-1993), Cedric A. B. Smith (1917-2002) y William Th. Tutte, los cuatro de Trinity, empezaron a construir rectángulos con disecciones perfectas mediante cuadrados utilizando el anterior método algebraico y a discutir sobre el problema de la cuadratura del cuadrado y el rectángulo. Entonces, relacionaron el problema de las disecciones cuadradas de los rectángulos con la teoría de las redes eléctricas de Kirchhoff (de lo que hablaremos en mi siguiente entrada en la sección Matemoción del Cuaderno de Cultura Científica), lo que les llevó finalmente a poder construir ejemplos de cuadraturas perfectas de cuadrados, tanto compuestas (es decir, con su-rectángulos perfectos), como simples.

En el artículo The Dissection of Rectangles into Squares (La disección de rectángulos en cuadrados), publicado en Duke Math. J. en 1940 se recoge toda esta investigación sobre las redes eléctricas, algunos de los ejemplos obtenidos y, en particular, el primer ejemplo de cuadratura perfecta y simple de un cuadrado de lado 5.468, de orden 55. Así mismo, se demuestra que el menor orden posible para la cuadratura perfecta de un rectángulo es 9 y que existen dos rectángulos con disecciones perfectas de orden 9.

David Singmaster recoge en Sources in recreational mathematics, an annotated bibliography que en las actas del Encuentro 203 de la Sociedad Matemática del Trinity (Cambridge) de marzo de 1939, Arthur Stone anunció, en el artículo de su conferencia Squaring the square, que Rowland Brooks había obtenido un ejemplo de cuadratura perfecta del cuadrado, de orden 39, que sería el primer ejemplo que demostraba que la conjetura de Luzin era errónea. Y en las actas del encuentro número 204, abril de 1939, Cedric Smith anunciaba que William Tutte había encontrado el primer cuadrado perfecto simple, de orden 55. Estos ejemplos se recogían en el artículo de 1940 de los cuatro de Trinity.

Aunque el primer artículo publicado con un contraejemplo a la conjetura de Luzin fue anterior al artículo de Brooks, Smith, Stone y Tutte de 1940, ya que fue publicado en la revista Mathematische Zeitschrift en 1939, por el matemático alemán Roland P. Sprague (1894-1967). Sprague construyó, a partir de los ejemplos de Zbigniew Moron, un rectángulo perfecto simple de orden 12 y otros cinco cuadrados, un cuadrado con una cuadratura perfecta, pero compuesta, de orden 55.

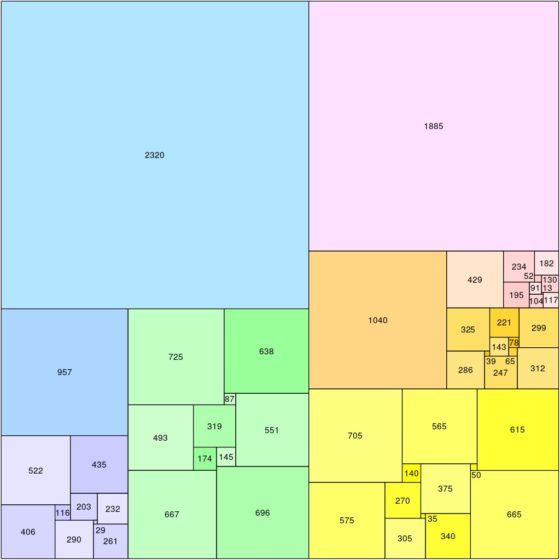
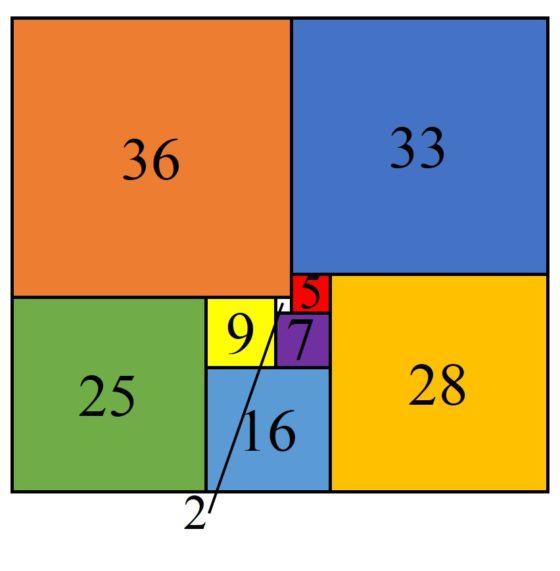
Poco a poco se fueron construyendo más ejemplos de cuadraturas perfectas de cuadrados, tanto compuestas, como simples. Por ejemplo, en 1948 el matemático británico Theophilus H. Willcocks (1912-2014) construyó una cuadratura perfecta de un cuadrado de orden 24, es decir, con tan solo 24 cuadrados, aunque era compuesta (véase la siguiente imagen). Durante mucho tiempo fue el orden más pequeño encontrado de una cuadratura perfecta de un cuadrado, de hecho, el orden 24 es el más pequeño posible para el caso de las cuadraturas compuestas.

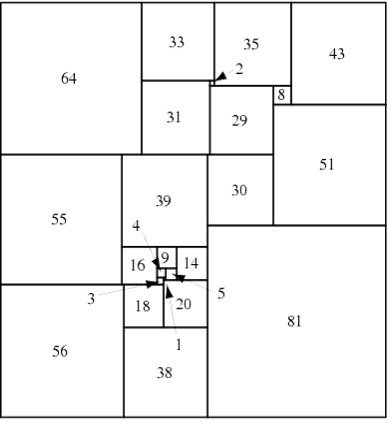
La llegada de los ordenadores cambió la investigación del problema de la cuadratura del cuadrado, permitiendo búsquedas más exhaustivas y la clasificación de todas las cuadraturas en función del orden. Es de destacar en esta nueva etapa la investigación de los matemáticos neerlandeses Christoffel J. Bouwkamp (1915 – 2003) y Adrianus J. W. Duijvestijn (1927-1998). En 1978, Duijvestijn descubrió la única cuadratura perfecta simple del cuadrado del orden más bajo posible, 21.

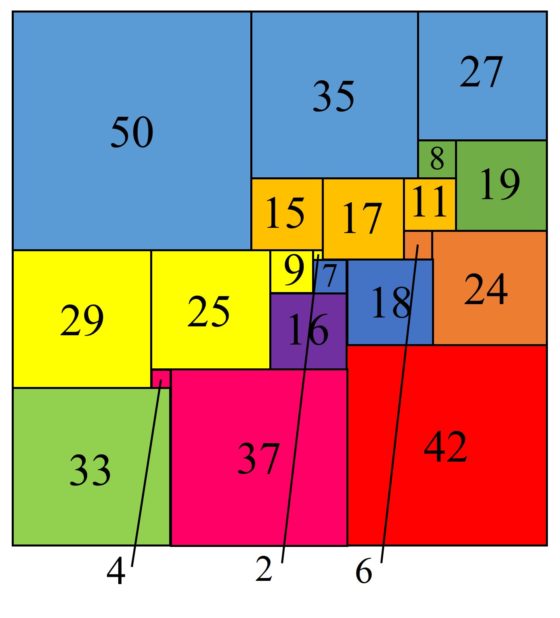
Antes de terminar esta entrada, expliquemos una notación sencilla, llamada código de Bouwkamp, que existe para describir las cuadraturas mediante cuadrados. En esta notación, se utilizan corchetes para incluir los cuadrados adyacentes que tienen el lado superior a la misma altura (horizontal) y los grupos de corchetes se van escribiendo desde el lado superior del cuadrado (o rectángulo) grande hacia abajo. Por ejemplo, la cuadratura perfecta simple del cuadrado de orden 21 descrita en la imagen anterior tiene el código de Bouwkamp [50, 35, 27], [8, 19], [15, 17, 11], [6, 24], [29, 25, 9, 2], [7, 18], [16], [42], [4, 37], [33].

Además, el número de cuadraturas perfectas del cuadrado de orden n, para n mayor o igual que 21, es la sucesión 1, 8, 12, 26, 160, 441, 1.152, 3.001, 7.901, … que en la Enciclopedia on-line de sucesiones de números enteros es la sucesión OEIS A006983.

Para terminar esta entrada del Cuaderno de Cultura Científica sobre el problema de la cuadratura (perfecta) del cuadrado, vamos a pensar en una disección muy particular, aquella en la que los lados de los cuadrados pequeños recorren todos los números naturales desde 1 hasta uno dado m. ¿Existirá una cuadratura como esta?

Si existiese esa cuadratura, el área del cuadrado grande, que será un número cuadrado N², sería la suma de las áreas de los cuadrados pequeños, que como están todos los lados desde 1 hasta m, sería la suma de los cuadrados de los cuadrados de los primeros m números naturales, es decir,

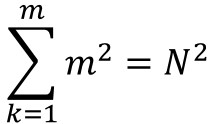
La suma de los cuadrados de los primeros números naturales es la sucesión de números que se conoce como números piramidales cuadrados (la sucesión OEIS A000330, de la Enciclopedia on-line de sucesiones de números enteros), pero solo hay un número piramidal cuadrado que sea el cuadrado de un número natural,´distinto de 1, el número 4.900 = 70², que es la suma de los cuadrados de los 24 primeros números naturales. Sin embargo, en 1974 se demostró, realizando una búsqueda exhaustiva por ordenador, que es imposible colocar los 24 cuadrados con lados de todos los tamaños entre 1 y 24 de manera que formen un cuadrado de lado 70.

Bibliografía

1.- Wolfram MathWorld: Perfect Square Dissection.

2.- Stuart Anderson, Tiling by squares

3.- David Singmaster, Sources in recreational mathematics, an annotated bibliography

4.- Henry Dudeney, Los acertijos de Canterbury, RBA, 2011.

5.- Sam Lyod, Los acertijos de Sam Loyd, RBA, 2011.

6.- Wikipedia: Scottish book

7.- Slanislaw Ulam, tradución al inglés del Scottish book

8.- Martin Gardner, The 2nd Scientific American Book of Mathematical Puzzles and Diversions, University of Chicago Press, 1987. Contiene el capítulo de W. Th. Tutte Squaring the square.

9.- Hallard T. Croft, Kenneth J. Falconer, Richard K. Guy, Unsolved Problems in Geometry, Springer-Verlag, 1991.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica