En la sección Matemoción del Cuaderno de Cultura Científica somos unos apasionados de la poesía, así como de la relación de esta con las matemáticas. Si miramos en el histórico de la misma podremos encontrar muchas entradas vinculando ambas, desde la serie Los números poéticos (primera parte, segunda parte y tercera parte) en la que se hablaba de poemas con temática matemática, como el poema sobre el número pi de la premio nobel de literatura polaca Wisława Szymborska o Los números oscuros de la poeta barcelonesa Clara Janés, hasta poemas en cuya estructura hay matemáticas, como poemas sobre una banda de Moebius (véase la entrada Poesía retorcida sobre la banda de Moebius), la combinatoria de la obra poética Cien mil millardos de poemas del escritor francés Raymond Queneau (véase 100 000 000 000 000 poemas) o el uso de la sucesión de Fibonacci, tanto en la obra Alfabeto de la poeta danesa Inger Christensen (véase ¡Nos encanta Fibonacci! ), como en los llamados poemas Fibonacci (véase Poemas Fibonacci).

Pero también hemos abordado el análisis matemático de algunas cuestiones relacionadas con la poesía, como en la entrada El origen poético de los números de Fibonacci, en la cual se muestra que la cantidad de estructuras posibles para versos con m moras (la mora es la “la unidad que mide el peso silábico, es decir, la duración de los segmentos fonológicos que componen la sílaba” y hay dos tipos de sílabas, unas cortas de una mora o instante silábico y otras largas de dos moras) es igual al número de Fibonacci F_{m + 1}.

En esta entrada del Cuaderno de Cultura Científica vamos a continuar con el análisis matemático de la poesía, en concreto, vamos a interesarnos por la cuestión de la métrica y a responder a la siguiente pregunta:

¿cuántas posibles estructuras de rimas existen para estrofas o poemas con un número fijo de versos?

Aunque sea una cuestión conocida, vamos a empezar por el principio. ¿Qué es la rima? Según el diccionario de la RAE es la “identidad de sonidos vocálicos y consonánticos, o solo vocálicos, a partir de la última vocal acentuada en dos o más versos”. Así, en el pareado final del poema Frases de la poeta argentina Alfonsina Storni (1892-1938),

Bravo león, mi corazón,
tiene apetitos, no razón

la rima es “ón”, luego rima consonante, mientras que en el pareado final del poema Lunes, miércoles y viernes del poeta andaluz Federico García Lorca (1898-1936)

Ante una vidriera rota
coso mi lírica ropa

la rima es “ota” y “opa”, luego rima asonante, ya que se repiten las vocales o-a.

Aunque la cuestión que nos interesa en esta entrada no es tanto si la rima es asonante o consonante, como analizar la cantidad de estructuras de rimas posibles para una estrofa, o poema, con un número fijo de versos. Por ejemplo, en una estrofa de dos versos hay dos posibilidades, que los dos rimen, como en el caso del pareado, que sería la estructura AA, o que no rimen, que sería la estructura libre AB, como en el haiku del poeta japonés Taneda Santoka (1882-1940)

Mi cuenco de mendigar
acepta hojas caídas

Por lo tanto, para estrofas o poemas con dos versos solo hay dos tipos de rima, AA y AB (en esta entrada vamos a escribir siempre la rima con letras mayúsculas, independientemente de que el verso sea de arte menor –de entre dos y ocho sílabas– o arte mayor –más de ocho sílabas–). Evidentemente, en el caso trivial de un solo verso solo hay una posibilidad trivial.

Pensemos ahora en la cantidad de estructuras rítmicas que son posibles en tercetos, es decir, en estrofas o poemas con tres versos. Por ejemplo, los haikus, que son pequeños poemas de origen japonés que habitualmente cuentan con tres versos, no suelen tener rima, luego ABC, como este poema del poeta donostiarra Karmelo C. Iribarren, titulado Domingo tarde.

Qué hago
mirando la lluvia
si no llueve

Por otra parte, la rima de la soleá andaluza es ABA, como en la siguiente soleá del poeta sevillano Antonio Machado (1875-1939).

Tengo un querer y una pena:
la pena quiere que viva;
el querer quiere que muera.

Se llama terceto monorrimo a aquellos tercetos que tienen la misma rima, ya sea asonante o consonante, en los tres versos, AAA, como en los tercetos del poema A Goya del poeta nicaragüense Rubén Darío (1867-1916), dentro de los Cantos de vida y esperanza. Así empieza el poema.

Poderoso visionario,
raro ingenio temerario,
por ti enciendo mi incensario.

Por ti, cuya gran paleta,
caprichosa, brusca, inquieta,
debe amar todo poeta;

por tus lóbregas visiones,
tus blancas irradiaciones,
tus negros y bermellones;

por tus colores dantescos,
por tus majos pintorescos,
y las glorias de tus frescos.

Otra rima posible para los tercetos es AAB, como en el poema La muerte de Melisanda del poeta chileno Pablo Neruda (1904-1973), cuyas estrofas son de dos versos (empieza así … A la sombra de los laureles / Melisanda se está muriendo.), salvo la anteúltima estrofa que es un terceto con rima AAB.

Por ella pisará las rosas,
perseguirá las mariposas
y dormirá en los cementerios.

Mientras que la rima ABB la encontramos por ejemplo en el siguiente poema de la poeta madrileña Gloria Fuertes (1917-1998).

En las noches claras,
resuelvo el problema de la soledad del ser.
Invito a la luna y con mi sombra somos tres.

Por lo tanto, hemos puesto ejemplos de todas las posibles rimas para estrofas o poemas con tres versos, AAA, AAB, ABB, ABA y ABC. Es decir, para tres versos son cinco las estructuras rítmicas posibles.

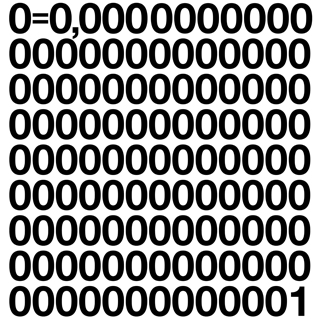
A continuación, analicemos cuántas son las estructuras posibles de rimas en las estrofas o poemas con cuatro versos. Empecemos con una composición poética clásica, el soneto, que consta de catorce versos separados en dos cuartetos y dos tercetos. Veamos un ejemplo clásico y jocoso de soneto del poeta y dramaturgo madrileño Lope de Vega (1562-1635).

Un soneto me manda hacer Violante,
que en mi vida me he visto en tanto aprieto;
catorce versos dicen que es soneto;
burla burlando van los tres delante.

Yo pensé que no hallara consonante,
y estoy a la mitad de otro cuarteto;
mas si me veo en el primer terceto,
no hay cosa en los cuartetos que me espante.

Por el primer terceto voy entrando,
y parece que entré con pie derecho,
pues fin con este verso le voy dando.

Ya estoy en el segundo, y aun sospecho
que voy los trece versos acabando;
contad si son catorce, y está hecho.

Como se ve en este ejemplo, los cuartetos de un soneto tienen rima ABBA, a la cual se la conoce como rima abrazada. A la estructura rítmica en la cual riman los cuatro versos AAAA se la conoce como continua o cuarteto monorrimo. Un ejemplo lo encontramos en el Libro del buen amor del Arcipreste de Hita (aprox. 1283-1350), en el capítulo Enxiemplo del garçón que quería casar con tres mujeres.

Era un garçón loco, mançebo bien valiente:
Non quería cassarse con una solamente;
Synon con tres mugeres: tal era su talente.
Porfiaron en cabo con él toda la gente.

Su padre é su madre é su hermano mayor
Afyncáronle mucho que ya por su amor
Con dos que se cassase, primero con la menor,
Dende á un mes conplido, casase con la mayor.

A la rima ABAB se la conoce como rima cruzada. Nos podemos encontrar ejemplos de esta rima en muchos poemas, por ejemplo, en el poema del poeta valenciano Miguel Hernández (1910-1942), titulado Niño yuntero, del que mostramos las primeras estrofas.

Carne de yugo, ha nacido
más humillado que bello,
con el cuello perseguido
por el yugo para el cuello.

Nace, como la herramienta,
a los golpes destinado,
de una tierra descontenta
y un insatisfecho arado.

Entre estiércol puro y vivo
de vacas, trae a la vida
un alma color de olivo
vieja ya y encallecida.

Releyendo algunos poemas del poeta portugués Fernando Pessoa (1888-1935), también he encontrado muchos cuartetos con rima ABAB, como el siguiente poema.

El poeta es un fingidor.
Finge tan completamente
que hasta finge que es dolor
el dolor que de veras siente.

Y quienes leen lo que escribe,
sienten, en el dolor leído,
no los dos que el poeta vive
sino aquél que no han tenido.

Y así va por su camino,
distrayendo a la razón,
ese tren sin real destino
que se llama corazón.

Pero también encontramos cuartetos con otras rimas, como AABA, en el poema que empieza así.

Siervo impasible de un fin desolado,
No creas o descreas demasiado.
Lo mismo da que pienses o no pienses.
Todo es irreal, anónimo, impensado.

Pero existen más estructuras rítmicas posibles para un cuarteto, AAAB, AABB, ABAA, ABBB, AABC, ABAC, ABCA, ABBC, ABCB, ABCC e incluso sin rima ABCD. En total, hay quince estructuras rítmicas para cuatro versos.

Lo siguiente sería obtener cuántas estructuras de rimas posibles hay para estrofas o poemas de cinco versos. Podéis listar vosotras mismas todas las posibilidades que existen y descubriréis que son 52, aunque nosotros vamos a aprovechar para utilizar unos diagramas muy especiales para mostrarlas.

En la novela clásica de la literatura japonesa El romance de Genji, de la escritora Murasaki Shikibu (aprox. 978-1014), aparecen representados con bonitos diagramas las 52 estructuras rítmicas posibles. Las líneas verticales con los versos de la estrofa o poema, y las líneas horizontales unen las líneas que riman. Cada capítulo, en total son 54, empieza con la imagen de uno de esos diagramas, aunque hay uno que se repite y otro extra. Los símbolos utilizados en El romance de Genji son los que aparecen en esta imagen.

Por ejemplo, el primer signo se correspondería con la rima ABACC, el número 37 con ABCAA o el número 52 con ABABA. Un ejemplo de rima ABABB, que es el diagrama 29 de la imagen anterior, es el poema Noche oscura del fraile y poeta castellano Juan de la Cruz (1542-1591), que empieza así:

En una noche oscura
con ansias, en amores inflamada,
¡oh dichosa ventura!
salí sin ser notada,
estando ya mi casa sosegada.

A oscuras, y segura,
por la secreta escala disfrazada,
¡Oh dichosa ventura!
a oscuras, y en celada,
estando ya mi casa sosegada.

Y podríamos seguir estudiando cuantas estructuras de rimas son posibles para estrofas o poemas de seis o más versos.

Si hacemos un balance de los resultados que hemos obtenido sobre cuántas posibles estructuras de rimas existen para estrofas o poemas con un número fijo n de versos, hemos visto que para los valores n = 1, 2, 3, 4 y 5, desde uno a cinco versos, la cantidad de posibles estructuras rítmicas son: 1, 2, 5, 15 y 52.

Estos son los cinco primeros términos de una sucesión importante de la combinatoria, los números de Bell (la sucesión A000110 en la Enciclopedia online de sucesiones de números enteros), que reciben su nombre del matemático y novelista estadounidense Eric Temple Bell (1883-1960), conocido por ser el autor del libro Los grandes matemáticos, de Zenón a Poincaré.

En combinatoria se define el número de Bell B_n como el número de posibles particiones de un conjunto de n elementos, es decir, la cantidad de formas distintas de distribuir los n elementos de un conjunto en grupos.

Si para todo número natural n se toma como conjunto de referencia el conjunto de los números naturales hasta n, {1, 2, …, n – 1, n}, calculemos las particiones posibles de ese conjunto y, por tanto, los números de Bell.

Para n = 1, solo hay una partición posible del conjunto {1}, la trivial, luego B₁ = 1;

para n = 2, las particiones del conjunto {1, 2}, es decir, las formas de distribuir los elementos de ese conjunto en grupos son {1}{2} y {1, 2}, por lo tanto, B₂ = 2;

para n = 3, las particiones de {1, 2, 3} son {1}{2}{3}, {1, 2}{3}, {1, 3}{2}, {2, 3}{1} y {1, 2, 3}, por eso B₃ = 5;

para n = 4, son {1}{2}{3}{4}, {1, 2}{3}{4}, {1, 3}{2}{4}, {1, 4}{2}{3}, {2, 3}{1}{4}, {2, 4}{1}{3}, {3, 4}{1}{2}, {1, 2}{3, 4}, {1, 3}{2, 4}, {1, 4}{2, 3}, {1, 2, 3}{4}, {1, 2, 4}{3}, {1, 3, 4}{2}, {2, 3, 4}{1} y {1, 2, 3, 4}, es decir, B₄ = 15;

de la misma forma podéis calcular las particiones de {1, 2, 3, 4, 5} y obtener que B₅ = 52. En general, los primeros miembros de la sucesión de números de Bell son

1, 2, 5, 15, 52, 203, 877, 4.140, 21.147, 115.975, …

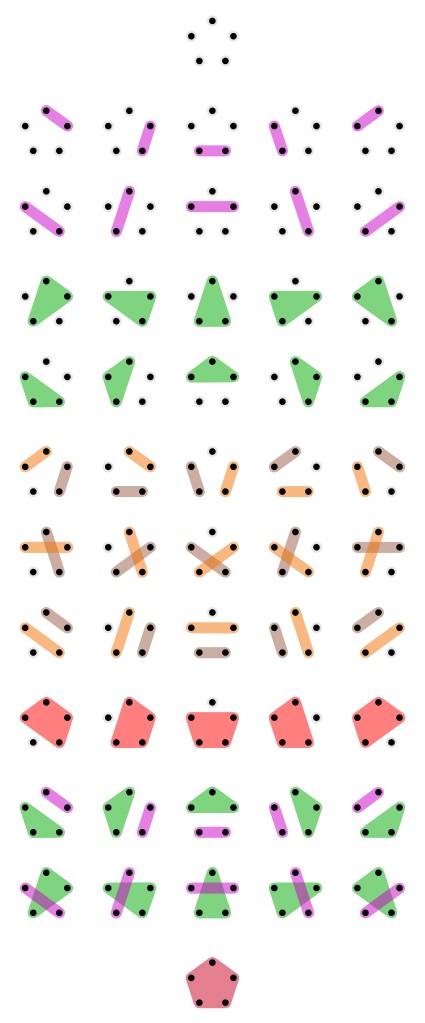
Como el conjunto sobre el que consideremos las particiones puede ser cualquiera, esto permite hacer diferentes diagramas e interpretaciones de los números de Bell. Por ejemplo, si se consideran puntos en el plano se pueden representar las particiones de estos como aparece en las siguientes imágenes, para B₃ y B₄.

Aunque si le metemos color a las particiones queda más bonito el diagrama, como la siguiente imagen para el cálculo de B₅.

Por otra parte, si un número N es producto de n números primos distintos, lo que se suele denominar un número libre de cuadrados, entonces B_n es igual al número de formas de expresar N como producto de divisores suyos, salvo el 1. Así, el número 105 puede expresarse como 105 = 3 · 5 · 7 = 15 · 7 = 21 · 5 = 35 · 3 (b₃ = 5). Notemos que el conjunto que se considera es el formado por los divisores primos del número N, en el caso de 105 sería {3, 5, 7}, y cada partición da lugar a una forma de expresar el número N como producto de divisores suyos, así la partición {3, 7}{5} da lugar a 105 = 21 · 5 , ya que 21 = 3 · 7.

Pero volviendo al tema central de esta entrada si ahora se toma el conjunto de los versos de una estrofa o poema con n versos para calcular el número de Bell B_n, entonces la cantidad de estructuras para las rimas de una estrofa o un poema de n versos es igual al número de Bell B_n, ya que se considera que los versos que están en un mismo grupo tienen la misma rima.

Si miramos a la sucesión de los números de Bell, B₇ = 877, es decir, existen 877 estructuras rítmicas para estrofas o poemas de 8 versos, entre las que están las rimas ABCBDAD, ABCBADA de las primeras estrofas del poema Nanas de la cebolla del poeta Miguel Hernández.

La cebolla es escarcha
cerrada y pobre:
escarcha de tus días
y de mis noches.
Hambre y cebolla:
hielo negro y escarcha
grande y redonda.

En la cuna del hambre
mi niño estaba.
Con sangre de cebolla
se amamantaba.
Pero tu sangre
escarchaba de azúcar,
cebolla y hambre.

Bibliografía

1.- Toni Prat, Poesía visual (blog)

2.- Raúl Ibáñez, La gran familia de los números (título provisional), Catarata, 2020.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica