Propiedades matemáticas del número 13
En el Cuaderno de Cultura Científica somos mucho de escribir sobre algunos números concretos, abordando cuestiones que van desde las matemáticas, la historia o curiosas anécdotas, hasta aplicaciones de los mismos o su uso en las artes.
Entre los números de los que hemos hablado están el número 3, en las entradas Las emocionantes aventuras del número tres (I) y Las emocionantes aventuras del número tres (II), el número 7, en la entrada El siete, un número muy popular, el número 9, en la entrada El número nueve en una noche de verano, el número 12, en la entrada El sistema duodecimal, o si los humanos hubiésemos tenido seis dedos en las manos, el número 22, en la entrada El misterioso número 22, el número de la Bestia, 666, en las entradas 666, el número de la Bestia (1) y 666, el número de la Bestia (2), entre algunos otros.

En las siguientes dos entradas, incluida esta, vamos a escribir sobre un número nefasto, que causa miedo o rechazo entre muchas personas, aunque para muchas otras es un número de la suerte, el número 13.
Un número primo singular
Aunque antes de meternos en creencias y supersticiones, que dejaremos para la siguiente entrada, empecemos con algunas de las propiedades matemáticas de este número. Una de las más evidentes es que es un número primo, es decir, un número que no se puede dividir más que por él mismo y por 1, como los números 2, 3, 5 o 7, pero no los números 4, 6 u 8, que se dividen, entre otros, por 2 (sobre los números primos podéis leer la entrada Buscando lagunas de números no primos).
Pero más aún, es un número que forma parte de curiosas parejas de números primos, como son los primos gemelos, parientes y sexis (sobre estas parejas de números primos pueden leerse las entradas Números primos gemelos, parientes y sexis (1) y Números primos gemelos, parientes y sexis (2)). Antes de nada, definamos estos conceptos matemáticos.
Como todos los números pares, a excepción del 2, son números compuestos, no primos, entonces lo más cerca que pueden estar dos números primos, salvo el 2 y el 3 que están pegados, es con solo un número par entre ellos. Y precisamente, a las parejas de números primos que están tan cerca, es decir, con solo un número par entre ellos o, dicho de otra forma, que la diferencia entre ellos es 2, se les llama números primos gemelos, como las parejas {3, 5}, {5, 7}, {11, 13} y {17, 19}. Por lo tanto, nuestro protagonista, el número 13, forma parte de una pareja de números primos gemelos.
Si los números primos gemelos son aquellas parejas de números primos tales que la diferencia entre ellos es 2, se van a llamar números primos parientes (“cousin” en inglés) a las parejas de números primos con una diferencia entre ellos de 4, como {3, 7}, {7, 11} o {13, 17}. En particular, el nefasto 13 forma parte de una pareja de números primos parientes.
Y se van a llamar números primos sexis a las parejas de números primos con una diferencia entre ellos de 6, como {5, 11}, {7, 13} o {11, 17}. El nombre de estas parejas de números no tiene nada que ver con lo sexual, sino que se debe a que la palabra en latín para el número “seis” es “sex”.
Más aún, el número 13 es lo que se denomina un número primo pitagórico. Si miramos a una primera definición, estos números son los primos de la forma 4n + 1. Aunque según el Teorema de Fermat de la suma de dos cuadrados, del matemático francés Pierre de Fermat (1601-1665), también conocido como Teorema navideño de Fermat (ya que está incluido en una carta dirigida al matemático francés Marin Mersenne (1588-1648) fechada el 25 de diciembre de 1640), los números primos pitagóricos serían aquellos números primos impares que pueden ser escritos como suma de dos cuadrados (de números naturales). En nuestro caso, 13 = 22 + 32. Por lo tanto, podemos considerar la raíz cuadrada de un número primo pitagórico como la hipotenusa de un triángulo rectángulo cuyos catetos sean números naturales, de ahí el término “pitagóricos”.
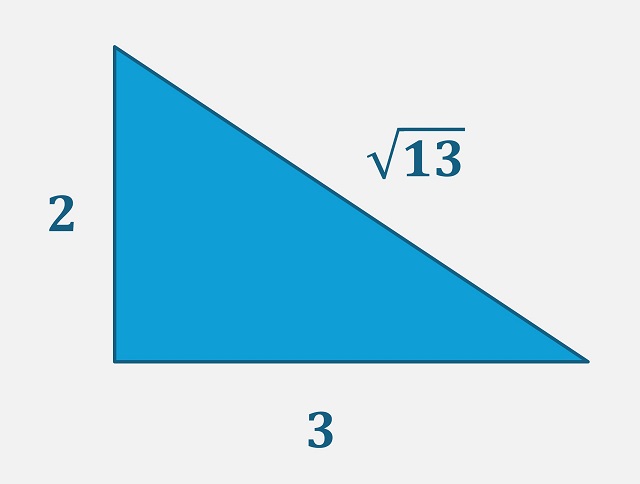
Mirando al teorema de Pitágoras
Siguiendo con el teorema de Pitágoras, podemos decir que el 13 forma parte de una terna pitagórica, de hecho, de dos ternas. Recordemos que se define una terna o triple pitagórico como un conjunto de tres números naturales (a, b, c) que satisfacen la ecuación del teorema de Pitágoras, a2 + b2 = c2. Las dos ternas pitagóricas que incluyen al número 13 son (5, 12, 13), siendo 13 la hipotenusa, y (13, 84, 85), siendo 13 el cateto menor.
Más aún, el número 13 es lo que se denomina un número congruente (sobre estos números podéis leer la entrada del Cuaderno de Cultura Científica titulada El teorema de Pitágoras y los números congruentes). Un número se llama congruente si es igual al área de un triángulo rectángulo cuyos lados, hipotenusa y catetos, son números racionales (recordemos que un número es racional si es el cociente p / q de dos números enteros p y q, como 0,5 = 1 / 2 ó 1,4 = 7 / 5). Por ejemplo, el triángulo egipcio, es decir, el triángulo rectángulo de lados (3, 4, 5), tiene área igual a 6, por lo tanto, el número 6 es un número congruente. Como puede verse en la siguiente imagen, los números 5, 6 y 7 son números congruentes (de hecho, los primeros).
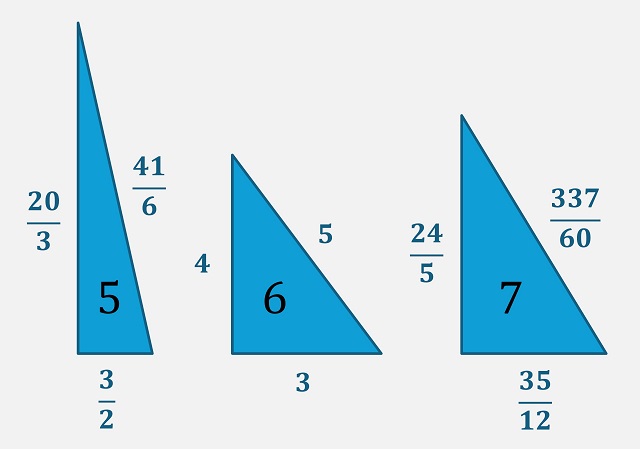
El problema de saber si un número es congruente (y calcular su triángulo rectángulo asociado) o no, es un problema antiguo, pero muy complejo, que está relacionado con las modernas curvas elípticas. Para que nos hagamos una idea la demostración de que 1 no es congruente no llegó hasta el siglo XVII, de la mano del jurista y matemático francés Pierre de Fermat (1601 – 1665). No vamos a abordar aquí esta compleja cuestión, pero sí vamos a mostrar cuál es el triángulo rectángulo de lados racionales cuya área es nuestro protagonista. Se trata del triángulo rectángulo cuyos catetos e hipotenusa son
780/323, 323/30 y 106921/9690.
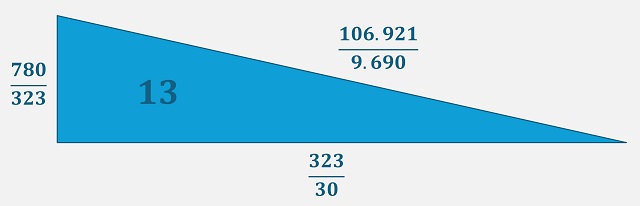
Un número de Fibonacci feliz
Aunque es un resultado más conocido, el número que en el sistema de numeración romano se escribe con una equis y tres palitos, XIII, forma parte de la conocida sucesión que empieza así
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …
que no es otra que la sucesión de Fibonacci, en la que cada término es la suma de los dos anteriores, Fn = Fn – 1 + Fn – 2, para n = 1, 2, 3, …
Esta es una sucesión infinita de números que aparece asociada al famoso problema de los conejos que Leonardo de Pisa (1170-1241), conocido como Fibonacci, plantea en su libro Liber Abaci / El libro del Ábaco, de 1202 (véase la entrada ¡Póngame media docena de fibonaccis!), pero también a la poesía en sánscrito en la India (como se explica en la entrada El origen poético de los números de Fibonacci).
El número 13 también es un número feliz. Como ya explicamos en la entrada Números felices para siempre, un número es feliz (en algunos textos también han sido llamados números elegantes) si al sumar los cuadrados de sus dígitos, repetir esta misma operación sobre el resultado obtenido e iterar el proceso suficientes veces, la sucesión de números resultante alcanza en algún momento el número 1. En caso contrario, se dice que el número es infeliz o triste. Por ejemplo, el número 7 es un número feliz ya que si consideramos la sucesión de resultados del algoritmo “sumar los cuadrados de sus dígitos” de manera recursiva nos queda lo siguiente:
7, 49, 97 (= 42 + 92), 130 (= 92 + 72), 10 (= 12 + 32 + 02), 1 (= 12 + 02),
En el caso del nefasto 13 se puede comprobar en tan solo dos pasos que es un número feliz, ya que la sucesión de resultados del mencionado algoritmo es 13, 10, 1.
El número atómico del aluminio, 13, no solo es un número feliz, sino que también es un “número de la suerte”, como explicamos en la entrada Los números de la suerte, que es otra interesante sucesión de números naturales, que pertenece a la familia de sucesiones de números generadas mediante “cribas”, como los primos si pensamos en la criba de Eratóstenes.
Una solución al problema de los collares de dos colores
Dentro de la matemática recreativa existe un problema conocido como el “problema del collar” que apareció en el libro Puzzles and Curious Problems / Rompecabezas y problemas curiosos (1932), del matemático recreativo británico Henry E. Dudeney (1857-1930). El problema dice así:
¿Cuántos collares diferentes se pueden hacer con ocho cuentas, en las que cada cuenta puede ser negra o blanca, y las cuentas solo se distinguen por su color?

Desde entonces se ha estudiado el problema general de collares con n cuentas, siendo n un número natural cualquiera, e incluso para k colores distintos, para k tomando también valores distintos dentro de los números naturales. Por ejemplo, se incluye en el libro New Mathematical Diversions / Nuevas diversiones matemáticas (1966), del gran divulgador de las matemáticas estadounidense Martin Gardner (1914-2010).
Hemos de aclarar que aquí se entiende que el collar se puede dar la vuelta (en tal caso se suele hablar también del problema de las pulseras). La respuesta al problema del collar con dos colores, para collares con n cuentas (n = 1, 2, 3, …), es 2, 3, 4, 6, 8, 13, 18, 30, 46, 78, … (en la siguiente imagen se muestra la solución para 6 cuentas, que es nuestro protagonista, el número 13). Esta sucesión de números naturales es la sucesión A000029 de la Enciclopedia on-line de sucesiones de números enteros.
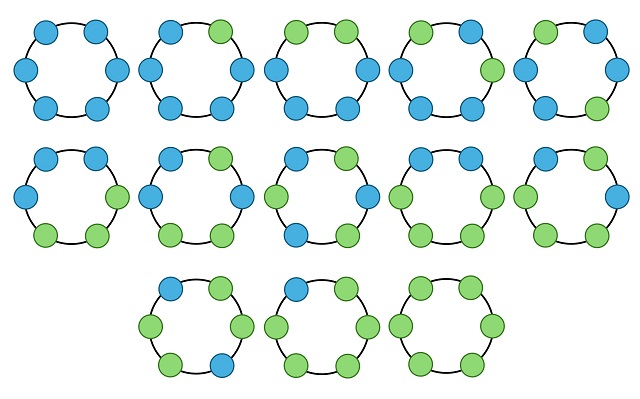
En el caso de que se considere que el collar no se puede dar la vuelta, entonces los dos collares de la siguiente imagen ya no serían iguales, mientras que el resto de los collares son iguales al darles la vuelta, por lo tanto, en este caso habría 14 collares distintos para 6 cuentas.
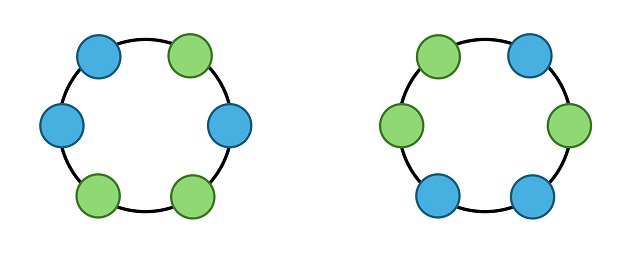
Por lo tanto, la solución al problema del collar con dos colores, para collares con n cuentas, si no se pueden voltear los collares, es la sucesión 2, 3, 4, 6, 8, 14, 20, 36, 60, 108, …, que es la sucesión A000031 de la Enciclopedia on-line de sucesiones de números enteros.
Un número poligonal centrado
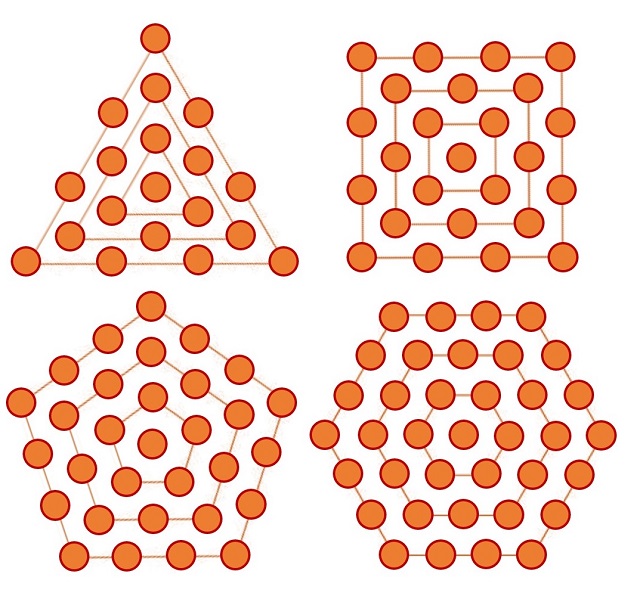
Los números poligonales (triangulares, cuadrados, pentagonales, hexagonales, etcétera) son aquellos números que se obtienen al representar el número como una disposición poligonal de puntos o piedras, como puede verse en la entrada El asesinato de Pitágoras, historia y matemáticas (y II). Sin embargo, existen otras disposiciones geométricas de puntos o piedras con forma poligonal, pero con un punto en el centro y los polígonos alrededor del mismo, son los números poligonales centrados (triangulares centrados, cuadrados centrados, pentagonales centrados, hexagonales centrados, etcétera), sobre los cuales hablamos en la entrada El problema de las flechas de Mahavira.
Como puede verse en la siguiente imagen, los primeros números triangulares centrados son 1, 4, 10, 19, los cuadrados centrados son 1, 5, 13, 25, los pentagonales centrados 1, 6, 16, 31 y los hexagonales centrados, llamados por Martin Gardner números hex, 1, 7, 19, 37. En particular, el número que se escribe como 111 en base 3, ya que 13 = 9 + 3 + 1 = 32 + 3 + 1, es un número cuadrado centrado.
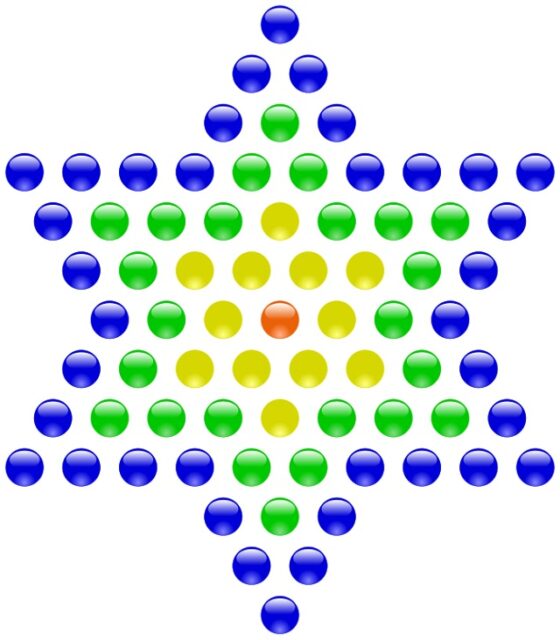
Más aún, el número considerado nefasto por muchas personas es también otro tipo de número poligonal centrado, en concreto, un número estrellado centrado, que es un número poligonal centrado cuya figura geométrica base es el el polígono estrellado de doce lados. En la siguiente imagen se muestran, utilizando distintos colores, los cuatro primeros números estrellados centrados, que son 1, 13, 37 y 73.
La despedida
Aunque podríamos incluir algunas propiedades matemáticas más, como que el número 13 en base 4 se representa con los mismos dígitos, pero cambiados de orden (son un anagrama), 31, puesto que 13 = 3 x 4 + 1, no conviene abusar, además las que hemos mostrado ya son lo suficientemente interesantes y curiosas.
Dejamos para la segunda parte de esta entrada del Cuaderno de Cultura Científica hablar sobre las supersticiones, creencias y miedos alrededor del número 13, un número que increíblemente ha sido eliminado de la numeración de los pisos de los hoteles, de las filas de los aviones o de las calles de algunas poblaciones. Aunque también es considerado un número de buena suerte, por ejemplo, para la cantante estadounidense Taylor Swift, que nació un día 13, cumplió 13 años un viernes 13, su primer álbum se convirtió en disco de oro en 13 semanas o ella misma afirma que cada vez que ha ganado un premio, estaba sentada en el asiento 13, en la fila 13, en la sección 13, o en la fila M (que es la decimotercera letra del alfabeto).
Bibliografía:
1.- Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.
2.- Página web: Numbers Aplenty.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
