
Hemos visto que la explicación de Einstein del efecto fotoeléctrico cuadra muy bien con las observaciones experimentales. Pero cuadra muy bien cualitativamente, es decir, explica lo que ocurre de forma genérica. Otra cosa muy distinta es que el modelo fotónico de Einstein explique cuantitativamente la observaciones. Solo entonces cabe hablar de un modelo realmente bueno.
Era necesario pues comprobar experimental y cuantitativamente el modelo de Einstein, en concreto dos afirmaciones claves:
a) La energía cinética máxima de los electrones es directamente proporcional a la frecuencia de la luz incidente; y
b) El factor de proporcionalidad h que relaciona la energía del fotón E con la frecuencia f (E = hf )es realmente el mismo para todas las sustancias.
Durante 10 años, los físicos experimentales intentaron realizar las pruebas cuantitativas necesarias. Una dificultad experimental era que el valor de la función de trabajo W para un metal cambia mucho si hay impurezas (por ejemplo, una capa de óxido del metal) en la superficie. Finalmente, en 1916, Robert A. Millikan estableció que existe una relación en forma de línea recta entre la frecuencia de la luz absorbida y la energía cinética máxima de los fotoelectrones, como lo exige la ecuación de Einstein.
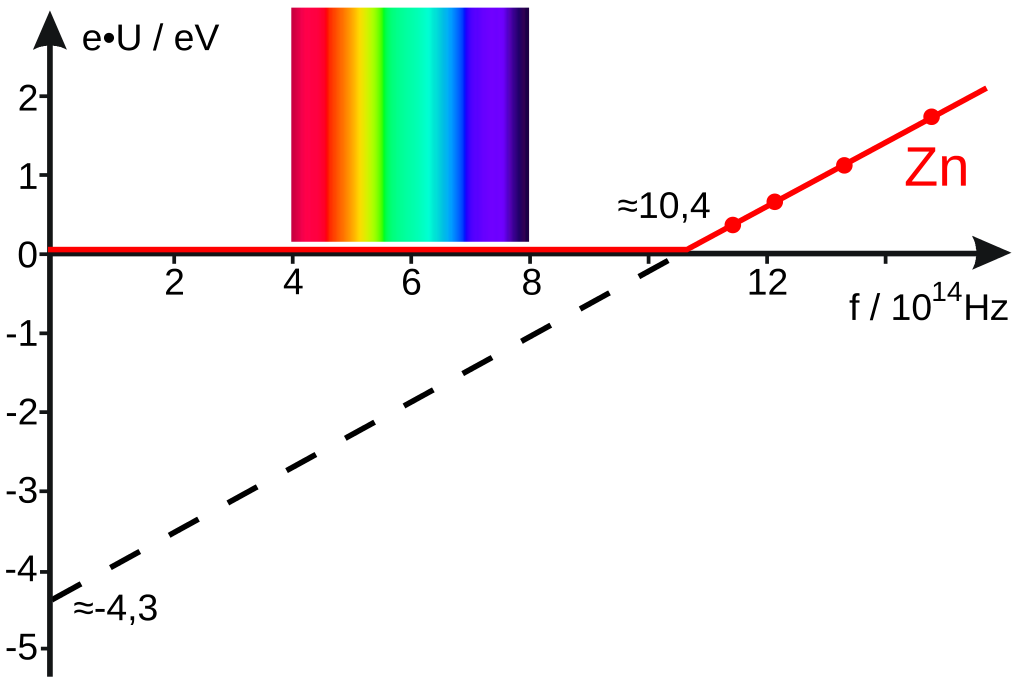
Si Ecmax se representa en el eje y y f a lo largo del eje x, entonces la ecuación de Einstein (Ecmax = hf – W) tiene la forma familiar de la ecuación para una línea recta y = mx + b. En una gráfica de la ecuación de Einstein, la pendiente debe ser igual a h, y la intersección con el eje y (f = 0) debe ser igual a -W. Esto es exactamente lo que encontró Millikan. Vemos en la imagen los datos para el zinc. La imagen es de Wikimedia Commons.
Para obtener sus datos, Millikan diseñó un aparato en el que la superficie fotoeléctrica del metal se obtenía por un corte en vacío. Un electroimán situado fuera de la cámara de vacío manipulaba una cuchilla dentro de la cámara para realizar los cortes. Este dispositivo, bastante complejo, era imprescindible para garantizar que se obtenía una superficie reproducible de metal puro.
Las líneas rectas que obtuvo Millikan para diferentes metales tenían la misma pendiente, h, aunque las frecuencias umbral (relacionadas con W) fuesen diferentes.
El valor de h obtenido a partir de los experimentos de Millikan eran, como hemos dicho, igual para distintos metales. De hecho también era el mismo encontrado por otros experimentos independientes. Este resultado sorprendió antes que ha nadie al propio Millikan, firme partidario de la teoría clásica de la luz. Su experimento demostró convincentemente que el modelo fotónico de la luz era correcto hasta donde se podía comprobar. El efecto fotoeléctrico dio como fruto dos premios Nobel, uno para Einstein por la teoría y otro para Millikan, por el experimento.

Pero, ¿qué era esta h?
Históricamente, la primera sugerencia de que la energía en la radiación electromagnética está «cuantificada» (viene en cantidades, cuantos, definidas) no aparece en el modelo fotónico del efecto fotoeléctrico. Lo hizo en estudios sobre el calor y la luz irradiados por los sólidos calientes. Max Planck introdujo el concepto de cuanto de energía (aunque en un contexto diferente) a finales de 1899, 5 años antes de la teoría de Einstein. Es por esto que a la constante h se la conoce como constante de Planck.
Planck trataba de explicar cómo la energía térmica (y la luz) irradiada por un cuerpo caliente está relacionada con la frecuencia de la radiación. La física clásica (termodinámica y electromagnetismo del siglo XIX) no podía explicar los hechos experimentales. Planck descubrió que los hechos solo podían interpretarse suponiendo que los átomos, al irradiar, cambian su energía no en cantidades variables continuas, sino en cantidades discretas, en paquetes. El modelo fotónico del efecto fotoeléctrico de Einstein puede considerarse como una extensión y aplicación de la teoría cuántica de Planck de la radiación térmica. La gran diferencia y punto esencial es que Einstein postuló que el cambio en la energía del átomo E que se transporta está localizada en un fotón de energía E = hf, donde f es la frecuencia de la luz emitida por el átomo, como si el fotón fuese una partícula, en lugar de estar repartida por toda la onda de luz.
El éxito del modelo fotónico del efecto fotoelectrico ponía a toda la comunidad científica ante un verdadero dilema. Según la teoría ondulatoria clásica, la luz consiste en ondas electromagnéticas que se extienden continuamente a lo largo del espacio. Esta teoría tuvo mucho éxito en la explicación de los fenómenos ópticos (reflexión, refracción, polarización, interferencia). La luz se comporta como una onda experimentalmente, y la teoría de Maxwell da buena cuenta de este comportamiento ondulatorio. Pero la teoría de Maxwell no puede explicar el efecto fotoeléctrico. La teoría de Einstein, que postula la existencia de cantidades discretas de energía luminosa, sí explica el efecto fotoeléctrico, pero no otras propiedades de la luz, como la interferencia.
O sea, que había dos modelos de luz cuyos conceptos básicos parecían contradecirse entre sí. Según uno la luz es un fenómeno ondulatorio; según el otro la luz tiene propiedades similares a las partículas. Cada modelo tenía sus éxitos y sus limitaciones. La solución de este problema tendría consecuencias enormes para toda la física y tecnologías modernas en general y para nuestra comprensión de los átomos en concreto.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El comportamiento corpuscular de la luz: momento lineal del fotón — Cuaderno de Cultura Científica
[…] descubrimiento del cuanto de energía en los primeros años del siglo XX proporcionó una explicación del efecto fotoeléctrico y […]