La distribución de velocidades moleculares de Maxwell
Armados con nuestro modelo simple y las ideas de Clausius, hay que empezar por el principio, esto es, por las volocidades que tendrán las moléculas y que determinarán su energía cinética.

No parece razonable que en un momento dado todas las moléculas en un gas tengan la misma velocidad. En 1859, Maxwell aplicó las matemáticas de la probabilidad a este problema. Propuso que las velocidades de las moléculas en un gas se distribuyen sobre todos los valores posibles. Eso sí, la mayoría de las moléculas tienen velocidades no muy alejadas de la velocidad media. Algunas tendrán velocidades mucho más bajas y otras pocas velocidades mucho más altas que la media.
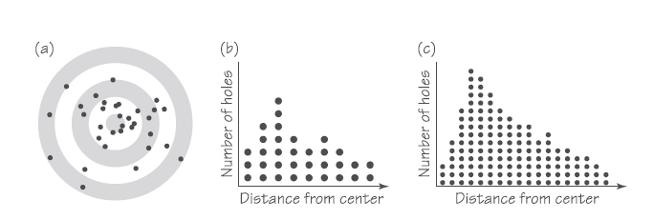
Un ejemplo simple ayudar a entender por qué la distribución de Maxwell de las velocidades moleculares se representa por curvas continuas, lo que es equivalente a explicar por qué Maxweel afirma que las velocidades se distribuyen en todas las velocidades posibles. Supongamos que una persona dispara flechas a una diana en un campo de tiro. Algunas flechas probablemente alcanzarán el centro de la diana, el blanco. Otras flechas darán en puntos más o menos alejados del blanco, como vemos en (a) en la figura de arriba. Si contamos el número de flechas diseminadas a diferentes distancias del blanco podemos construir un gráfico muy sencillo como el que se presenta en (b). Este gráfico muestra la distribución de los agujeros hechos por los impactos de las flechas en función de la distancia al blanco para un conjunto de unas pocas decenas de disparos. Si repetimos el experimento para un número mucho mayor de disparos, obtendremos una distribución como la de (c). Si el número de disparos fuese incluso mucho mayor la diferencia en la distancia al blanco que podríamos considerar con un número significativo de impactos sería mucho menor. En el límite, para un número extremadamente grande de disparos habría un número significativo de los mismos prácticamente para cualquier distancia que pudiésemos medir. Por analogía, al ser el número de moléculas en un gas, de hecho, realmente enorme, el gráfico que muestra la distribución de las velocidades moleculares es continuo a cualquier escala que se pueda dibujar.
La forma exacta que toma la curva que se forma cuando la distribución (c) se lleva a valores muy altos viene determinada por muchas cosas que tienen que ver con el arco (dimensiones, materiales, estado), las flechas (materiales, dimensiones), la persona (pericia, fortaleza, estado de salud), y así sucesivamente. Otros procesos dan lugar a otras formas de curvas. Las velocidades de las moléculas en un gas están determinadas por las colisiones que tienen entre sí. Maxwell utilizó un inteligente argumento matemático para deducir cuál debería ser la distribución de las velocidades moleculares y que da lugar a curvas para un gas concreto en función de la temperatura como vemos en la imagen siguiente.
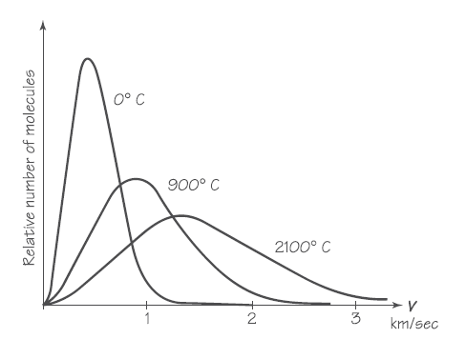
Para un gas a cualquier temperatura dada, la «cola» de cada curva es mucho más larga a la derecha (alta velocidad) que a la izquierda (velocidades bajas). A medida que la temperatura aumenta, el pico de la curva se desplaza a velocidades más altas y la distribución de la velocidad se vuelve más amplia.
Todo esto está muy bien, pero tenía que demostrarse experimentalmente que era correcto para que fuese de alguna utilidad. Hubo que esperar más de 60 años para que pudieran realizarse mediciones directas en los años veinte del siglo pasado. Otto Stern diseñó un método realmente ingenioso para medir las velocidades de un haz de moléculas. Los experimentos de Stern* y otros investigadores demostraron que las velocidades moleculares se distribuyen según calculó Maxwell.
Nota:
*Este resultado hubiese sido la confirmación de la teoria cinética y de la existencia de las moléculas si la teoría sobre el movimiento browniano de Einstein no hubiese sido probada experimentalmente por Perrin en 1908.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Iñaki
No soy experto en fisica, pero si hay aspectos de fisica que me fascinan. Hace unos dias leyendo un libro de G. Gamow (biografía de la fisica) quede intrigado en un aspecto de la ondas electromagneticas que he entendido tras preguntar en un foro de fisica donde hago preguntas. Ahora viene este artículo Maxwell me persigue ¿tendré alguna pesadilla con algún diablo?
Hitos en la red #182 | Enlace Recomendado | Naukas
[…] La distribución de velocidades moleculares de Maxwell […]
El tamaño de las moléculas – Cuaderno de Cultura Científica
[…] que llegó la prueba de que las ideas de Maxwell sobre la distribución de las velocidades de las moléculas eran correctas aparecieron no pocas cuestiones, muchas muy razonables, a las que se tuvo que […]
La ley del gas ideal a partir del modelo cinético – Cuaderno de Cultura Científica
[…] exponer nuestro modelo simple del gas ideal, incorporar la distribución de las velocidades de las moléculas de Maxwell y tener en cuenta el efecto del tamaño de las moléculas, ya lo tenemos todo para ver […]
El demonio de Maxwell – Cuaderno de Cultura Científica
[…] en la otra. “Ahora concibe un ser finito”, sugirió Maxwell, “que conoce las trayectorias y las velocidades de todas las moléculas, pero que no puede hacer otro trabajo que no sea abrir y cerrar un agujero en el diafragma”. Este […]
¿Por qué cuando subimos una montaña hace más frío?
[…] resulta que la densidad del aire es clave para la temperatura. Cuando las moléculas de un gas están más juntas, chocan más entre sí y pueden transferir mejor la energía térmica. En […]