Las ideas de Balmer sobre el espectro del hidrógeno tuvieron un éxito enorme. Veámoslo.

Para usar la notación moderna, reescribimos la fórmula de Balmer λ = b [n²/(n²-2²)] en una forma que nos será más útil:

1/λ = R_H (1/2² – 1/n²)

En esta ecuación que, como decimos, puede derivarse de la anterior, R_H es una constante, igual a 4 / b. Se llama constante de Rydberg para el hidrógeno, en honor del espectroscopista J.R. Rydberg. Continuando el trabajo de Balmer, Rydberg hizo un gran progreso en la búsqueda de varias series espectrales. La serie de líneas descritas por la fórmula de Balmer se llama la serie de Balmer. Balmer construyó su fórmula a partir de las longitudes de onda conocidas de solo cuatro líneas en la parte visible del espectro. Esta fórmula de Balmer predice correctamente cada una de estas cuatro líneas con una precisión considerable. La fórmula, sin embargo, parecía indicar que podrían existir muchas más líneas en la misma serie [1]. Además,

La sugerencia especulativa [2] de Balmer de reemplazar 2² por otros números ofrece las siguientes posibilidades:

1/λ = R_H (1/1² – 1/n²)

1/λ = R_H (1/3² – 1/n²)

1/λ = R_H (1/4² – 1/n²)

…

Cada una de estas ecuaciones describe una posible serie de líneas de emisión. Todas estas series hipotéticas de líneas pueden resumirse en una fórmula general

1/λ = R_H (1/n_f² – 1/n_i²)

donde n_f sería un número entero que es fijo para cada serie para la que se encuentren longitudes de onda (por ejemplo, n_f = 2 para todas las líneas de la serie Balmer). Por otro lado n_i representa enteros que toman los valores n_f + 1, n_f + 2, n_f + 3,. . . para las sucesivas líneas individuales en una serie dada (las cuatro primeras líneas de la serie de Balmer, n_i toma por tanto los valores 3, 4, 5, y 6) La constante R_H debe tener el mismo valor para todas las series del hidrógeno.

Reiteremos que todo esto es pura especulación [2]. No hay nada que indique que deba existir ninguna otra serie, ninguna línea que se ajuste a la fórmula general, excepto la serie de Balmer observada experimentalmente, donde n_f = 2. Pero resultó que, cuando la comunidad científica se puso a buscar estas líneas hipotéticas con buenos espectrómetros descubrió que, de hecho, ¡existen!

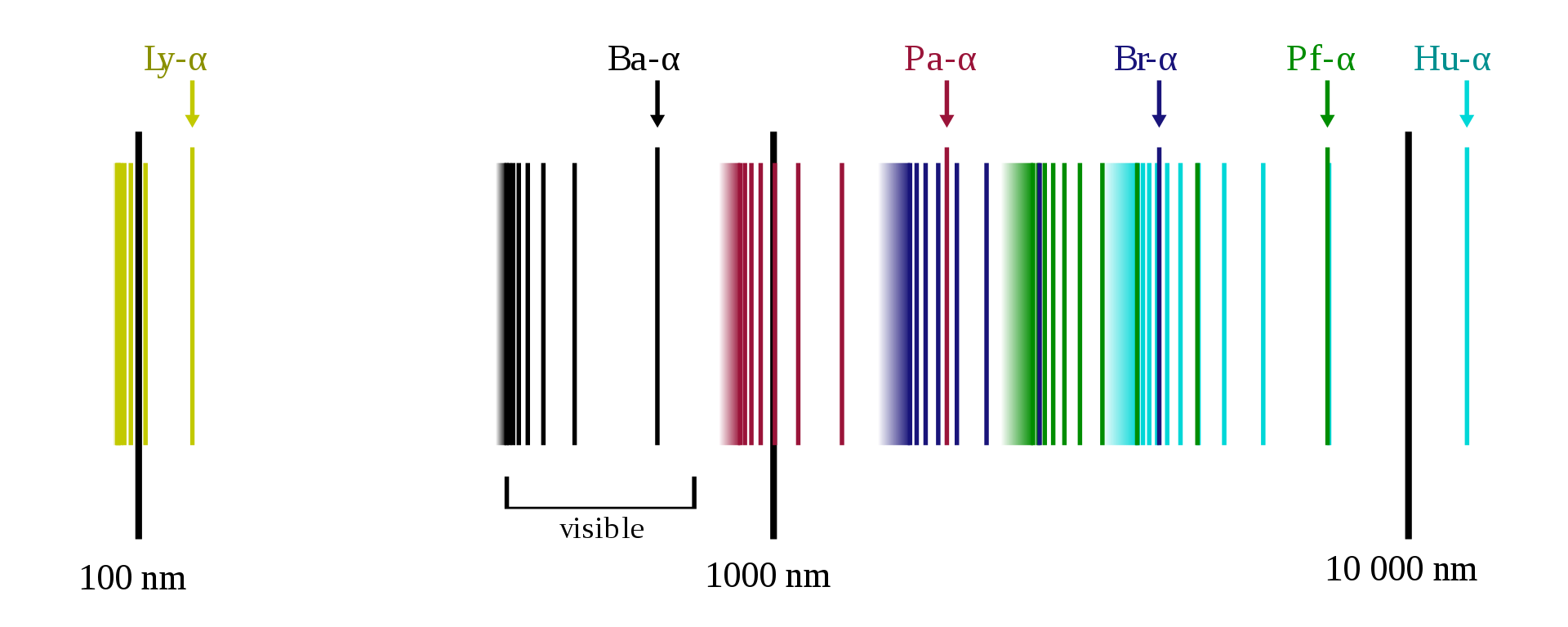
En 1908, F. Paschen encontró dos líneas del hidrógeno en el infrarrojo. Sus longitudes de onda se correspondían con notable precisión a la fórmula general estableciendo n_f = 3 y n_i = 4 y 5. Desde entonces, se han identificado muchas otras líneas en esta «serie de Paschen». Con técnicas y aparatos experimentales mejorados, se pudieron explorar nuevas regiones del espectro. Así, se fueron agregando gradualmente otras series a las series de Balmer y de Paschen. Las series del espectro del hidrógeno descubiertas son las siguientes (entre paréntesis año de descubrimiento):

Lyman (1906–1914) n_f =1, n_i = 2, 3, 4, . . . en el ultravioleta;

Balmer (1885) n_f = 2, n_i = 3, 4, 5, . . . en el ultravioleta-visible;

Paschen (1908) n_f = 3, n_i = 4, 5, 6, . . . en el infrarrojo;

Brackett (1922) n_f = 4, n_i = 5, 6, 7, . . . en el infrarrojo;

Pfund (1924) n_f = 5, n_i = 6, 7, 8, . . . en el infrarrojo;

Humphreys (1953) n_f = 6, n_i = 7, 8, 9, . . .en el infrarrojo.

Balmer también especuló con la idea de que su fórmula para el espectro del hidrógeno pudiera ser un patrón para encontrar relaciones en los espectros de otros gases. Esta sugerencia también dio fruto. La fórmula de Balmer en sí misma no funcionó directamente para describir espectros de gases distintos al hidrógeno. Pero sí inspiró fórmulas de forma matemática similar que describieron con éxito el orden en porciones de muchos espectros complejos [3].

Para sorpresa de muchos y desesperación de otros no se podía construir ningún modelo basado en la mecánica clásica y el electromagnetismo que explicara los espectros descritos por estas fórmulas.

Lo que ya hemos visto sobre la teoría cuántica sugería una línea de ataque. Obviamente, la emisión y absorción de luz de un átomo debe corresponder a una disminución y un aumento de la energía del átomo. Si los átomos de un elemento emiten luz de solo ciertas frecuencias, entonces la energía de los átomos debe poder cambiar solo en ciertas cantidades. Estos cambios de energía deben implicar la reorganización de las partes del átomo. Se hacía imprescindible cambiar radicalmente el enfoque a la hora de construir un modelo de átomo viable. Pero era necesario un ingrediente fundamental adicional antes de que se construyese un modelo atómico que pudiese tener éxito: el descubrimiento de que el átomo es, básicamente, espacio vacío.

Notas:

[1] De hecho, infinitas, ya que n = 3, 4, 5, 6, 7, 8,… ∞

[2] Y numerológica. Es por pura simetría matemática. Funciona porque funciona, pero recordemos que tras la sugerencia de Balmer no hay ninguna base física a priori.

[3] La constante de Rydberg R_H también reapareció en estas fórmulas empíricas.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance