Hemos visto que los experimentos mentales de Galileo con mariposas y pelotas de baloncesto en un barco nos decían que para una persona en un marco de referencia, ya esté éste en reposo o en movimiento uniforme, no hay forma de determinar la velocidad de dicho marco de referencia en el que está haciendo experimentos mecánicos si los hace en ese marco de referencia. Todo lo que ocurre en el marco de referencia ocurre como si estuviese en reposo.

Pero, ¿cómo lo ve alguien fuera del marco de referencia? Supongamos que dejas caer una pelota en un marco móvil. Para ti, montado en el marco móvil, un barco que navega por un río tranquilo, por ejemplo, parece caer directamente al suelo. Pero, ¿cómo ve el movimiento de la pelota alguien que no se mueve contigo? ¿Cómo lo ve tu amiga que está en la orilla del río cuando pasa tu barco? Otra forma equivalente de realizar el experimento es que tu amiga esté quieta mientras tú caminas a velocidad uniforme botando la pelota. ¿Qué ves tú y qué ve ella?

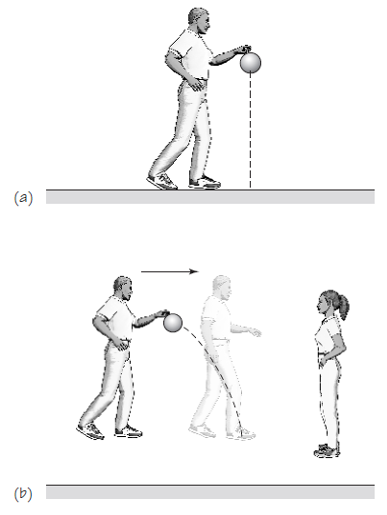
Si nos fijamos, en ambos casos tu amiga notará que, desde su punto de vista, la pelota no cae y sube en línea recta. Por el contrario, la pelota sigue la trayectoria parabólica de un proyectil, con una velocidad uniforme en la dirección horizontal (la del barco o la tuya caminando), así como una aceleración uniforme en la dirección vertical.

Este experimento tan simple lleva al sorprendente resultado de que dos personas diferentes en dos marcos de referencia diferentes describen el mismo hecho de dos maneras diferentes. Mientras caminas o pasas navegando, estás en un marco de referencia con respecto al cual la pelota está en reposo antes de ser liberada. Cuando la sueltas, la ves cayendo en línea recta a tu lado y aterriza a tus pies. Pero la persona que te observa, en su propio marco de referencia, dirá que ve algo completamente diferente: una pelota que comienza contigo, no en reposo sino en movimiento uniforme, y al soltarla se mueve, no en línea recta, sino trazando una parábola hacia el suelo, impactando en el suelo a tus pies. Además, esto es exactamente lo que esperaría ver, ya que la bola comenzó moviéndose horizontalmente y luego debe trazar la trayectoria curva de un proyectil que cae por efecto de la gravedad.

Entonces, ¿quién tiene razón? ¿La bola cae directamente hacia abajo o sigue la trayectoria curva de un proyectil? La respuesta de Galileo fue: ambos tenéis razón. ¿Pero cómo puede ser eso? ¿Cómo puede haber dos observaciones diferentes y dos explicaciones diferentes para un mismo hecho físico, una pelota cayendo a los pies de alguien?

La respuesta es que observadores diferentes observan el mismo evento de manera diferente cuando están observando el evento desde diferentes marcos de referencia en movimiento relativo. La bola comienza estacionaria con respecto a un marco (el tuyo), mientras que, hasta su liberación, está en movimiento constante (uniforme) en relación con el otro marco de referencia (el de tu amiga). Ambos observadores ven que todo sucede como cabe esperar de las leyes de Newton aplicadas a su situación [1]. Pero lo que ven es diferente para cada observador. Dado que no existe un marco de referencia absoluto (ningún marco de referencia en velocidad uniforme es mejor o preferible a cualquier otro que se mueva con velocidad uniforme), no hay movimiento absoluto, y las observaciones hechas por ambos observadores son igualmente válidas.

Galileo se dio cuenta de que la persona que está en reposo con respecto a la pelota no puede determinar mediante ningún experimento mecánico que implique pelotas que caen, planos inclinados, etc., si está en reposo o en movimiento uniforme en relación con cualquier otra cosa, ya que todos estos experimentos ocurrirán como si simplemente estuviera en reposo. Una bola que cae desde una torre en la Tierra en movimiento golpeará la base de la torre como si la Tierra estuviera en reposo. Dado que nos movemos con la Tierra, siempre que se pueda considerar que la Tierra se mueve con velocidad uniforme [2], no hay ningún experimento mecánico que nos permita determinar si estamos o no realmente en reposo o en movimiento uniforme.

Notas:

[1] Las observaciones de los acontecimientos dependen de los marcos de referencia pero no así las leyes de la mecánica. Las leyes son las mismas (en otras palabras, son invarientes) en los marcos de referencia que están en movimiento uniforme relativo o en reposo. Todos los objetos que observamos que se mueven con respecto a nosotros siguen las mismas leyes de la mecánica. Por ello, de igual forma que esto se llama principio de relatividad de Galileo, podría llamarse principio de invariancia de Galileo.

[2] Descartamos por despreciable y a efectos del ejemplo el hecho de que durante el breve período de tiempo del experimento la Tierra en realidad gira, lo que es un cambio de dirección y, por tanto, un cambio en la velocidad o, lo que es lo mismo, una aceleración.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance