Veamos qué le ocurre a la medición del tiempo cuando se tiene en cuenta la teoría de la invariancia. Para ello seguiremos el argumento original de Einstein, que es sorprendentemente simple, puesto al día con la tecnología actual. Es tan simple que para llegar a la conclusión que buscamos lo más complejo desde el punto de vista matemático que se usa (nosotros no lo haremos) es el teorema de Pitágoras y álgebra de primaria.

En este experimento, una observadora, Mónica, está en una nave espacial moviéndose a una velocidad uniforme extremadamente rápida y en línea recta en relación con otra nave en la que está Esteban, que permanece estacionario. En la nave espacial de Mónica (es decir, en su marco de referencia) hay un reloj que mide el tiempo en intervalos precisos mediante el uso de un pulso de láser. El pulso viaja directamente desde un láser, golpea un espejo y se refleja. Cuando el pulso regresa al punto inicial, es detectado por un fotosensor, que registra entonces el tiempo transcurrido, al que llamaremos Δt_m (que se corresponde con el tiempo de ida y vuelta al espejo, por tanto), y emite otro pulso. Como la velocidad de la luz es constante y la distancia que recorre es fija, el segundo pulso tarda exactamente la misma cantidad de tiempo Δt_m para realizar el viaje de ida y vuelta según Mónica. Son estos intervalos de tiempo idénticos los que se usan como un reloj, tic-tac, tic-tac, para medir el tiempo en la nave de Mónica.

Dado que Mónica viaja a una velocidad uniforme, el principio de relatividad de Einstein le dice que el reloj se comporta exactamente como lo haría si estuviera en reposo. De hecho, de acuerdo con este principio, ella no podría decir a partir de este experimento (o de cualquier otro) si su nave está en reposo o en movimiento en relación con Esteban sin mirar hacia fuera de la nave espacial. Pero para Esteban, que no está en marco de referencia de Mónica, sino en el suyo propio, le parece que avanza rápidamente en línea recta con respecto a él. (Por supuesto, podría ser que Esteban fuese quien se mueve hacia atrás, mientras que Mónica está estacionaria, pero la observación y el argumento que sigue serían los mismos).

Al observar el reloj láser de Mónica mientras su nave espacial pasa volando a su lado, ¿qué ve Esteban? Al igual que en el experimento de la relatividad galileana con la pelota que cae al suelo cuando la suelta una persona en movimiento, Esteban ve algo muy diferente de lo que ve Mónica. Debido a que la nave espacial de ella se está moviendo con respecto a la de él, observa que el pulso de luz sigue una trayectoria en diagonal hacia el espejo y otra trayectoria diagonal hacia el detector. Usaremos el símbolo t_e para el tiempo que mide Esteban.

Aquí es donde entra el segundo postulado de Einstein: la velocidad de la luz, c, medida debe ser la misma independientemente de que la observe Mónica o Esteban. Pero la distancia que recorre el pulso de luz durante un viaje de ida y vuelta tal y como lo ve Mónica es más corta de la que ve Esteban. Si llamamos d_m a la distancia total que recorre el pulso desde el emisor hasta el espejo y vuelta para Mónica y d_e para Esteban, podemos escribir que c = d_m/Δt_m = d_e/Δt_e

Como d_e es mayor que d_m, Δt_e debe ser mayor que Δt_m, para que las proporciones tengan el mismo valor, c. Esto significa que el intervalo de tiempo (Δt_e ) para el viaje de ida y vuelta del pulso de luz, registrado en el reloj como Esteban lo observa, es más largo que el intervalo de tiempo (Δt_m ) registrado en el reloj cuando es Mónica la que lo observa.

La conclusión sorprendente de este experimento mental (que en realidad es una deducción a partir de los postulados de la teoría de la invariancia) es:

Los intervalos de tiempo no son absolutos e invariables, sino relativos. Cualquier fenómeno repetitivo que se mueva con relación a un observador estacionario (como un reloj como el de Mónica), parece para el observador estacionario que transcurre más lentamente de lo que parece hacerlo cuando lo mide el observador que se mueve con el reloj, y tanto más despacio cuanto más rápido se mueva. Esto se conoce como dilatación del tiempo.

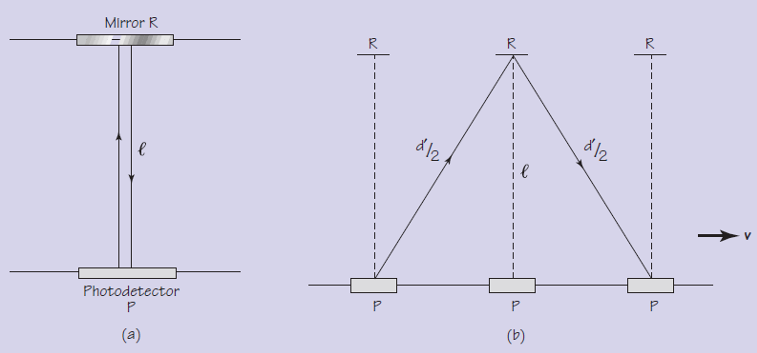
Pero, ¿cuánto más lento parece un reloj que se mueve respecto de un observador? Para obtener la respuesta, se puede usar el gráfico de arriba y usar el teorema de Pitágoras. Con un poco de álgebra básica, se obtiene la relación exacta entre el intervalo de tiempo transcurrido registrado por un reloj que está estacionario con respecto al observador (como en el caso de Mónica) y el intervalo de tiempo transcurrido para el mismo fenómeno medido por alguien que observa el reloj en movimiento a una velocidad constante v (como en el caso de Esteban).

El resultado viene dado por una ecuación muy sencilla, Δt_e = Δt_m /√(1-v²/c²), que viene a decir que el intervalo de tiempo que observa Esteban es diferente del intervalo de tiempo que observa Mónica para el mismo reloj, estacionario en el marco de referencia de ella, por el efecto de la velocidad constante v con la que Esteban observa que se mueve el marco de referencia de Mónica, su nave y todo lo que ésta contiene, incluido el reloj. Este efecto lo introduce el denominador √(1-v²/c²).

En la próxima entrega analizaremos en detalle esta ecuación.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance