La teoría general de la relatividad hemos visto que se basa, de forma análoga a la especial, en dos principios básicos: el de equivalenvia y el de covariancia. También hemos podido apreciar lo fácil e intuitivo que es enunciarlos. Otra cosa muy diferente es expresarlos matemáticamente y las consecuencias que se derivan de ellos son impresionantes, paradójicas y no fácilmente aprehensibles. Por ello, aunque la tentación sea obviar todo el aspecto matemático, no podemos dejar de pasar muy por encima por él y tener una idea de, al menos, el aspecto que tienen las llamadas ecuaciones del campo de Einstein [1][2].

Einstein empleó varios años y muchas discusiones y trabajos con matemáticos, especialmente Marcel Grossman y David Hilbert, para poder lograr la expresión matemática de sus ideas. Aunque Einstein ya dispuso de un primer esbozo en 1911 no sería hasta finales de 1915 que encontrase la forma definitiva [3]. La ecuaciones de campo se presentaron a la Academia Prusiana de Ciencias en noviembre de 1915. La idea general es que las soluciones a estas ecuaciones indican cómo el espaciotiempo y la masa-energía se influyen el uno a la otra y viceversa. Por ejemplo, cómo afecta al espaciotiempo la presencia de una masa como la del Sol, y cómo este espaciotiempo afecta al movimiento de una masa menor en las proximidades del Sol, como la de un planeta; o qué le pasa al espaciotiempo cuando una estrella masiva colapsa sobre sí misma hasta crear un punto de densidad infinita.

La dificultad matemática que encontró Einstein estriba en expresar cuantitativamente que el espaciotiempo se curva y cómo lo hace. Para conseguirlo tuvo que aprender las bases toda una rama de las matemáticas: el cálculo tensorial.

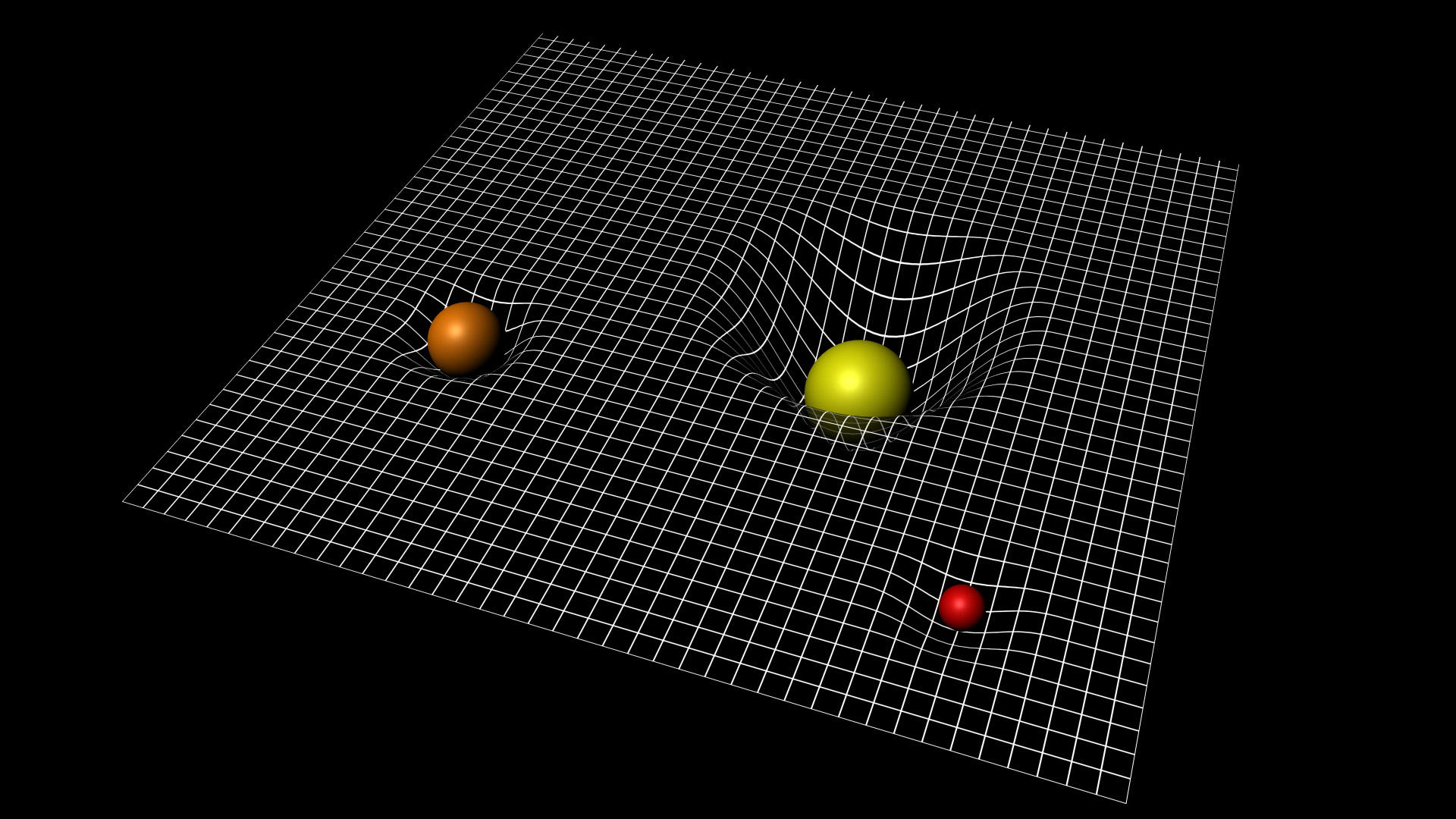
El espaciotiempo se curva

Si cortas una naranja por la mitad, quitas la pulpa del interior, e intentas aplanar el hemisferio de piel resultante, terminas rajándolo. Si tratas de aplanar algo con la forma de una silla de montar, como una patata frita (de las de bolsa) revenida, te encuentras con el problema contrario: hay “demasiada” superficie y se te forman pliegues. Si coges, sin embargo, un rollo de papel de cocina y deseas aplanarlo, no hay nada más fácil, con desenrollarlo, listo. Las superficies como las esferas se dice que están curvadas positivamente, las que tienen la forma de una silla de montar que lo están negativamente, y las que son como el papel de cocina son, simplemente, planas (démonos cuenta que son planas en este sentido aunque no estén en un plano). Esto es así porque la curvatura se define en términos de “geometría intrínseca” de una superficie, en la que la distancia se mide en función de los caminos que están dentro de la superficie.

Hay varias formas de hacer precisa esta noción de curvatura y hacerla cuantitativa, de tal manera que a cada punto de la superficie se pueda asociar un número que diga “cómo de curvada” está en ese punto. Para poder hacer esto es necesario que se cumplan determinadas condiciones matemáticas que permitan determinar las longitudes de los caminos, es lo que se llama una métrica riemanniana. La noción de curvatura puede ser generalizada a un mayor número de dimensiones, de tal forma que se habla de la curvatura en un punto en una variedad riemanniana de d dimensiones. Sin embargo, cuando la dimensión es mayor de dos, es decir, no es un plano lo que se curva sino un espacio, las posibilidades de curvatura en un punto se hacen tan complicadas que ya no pueden ser expresadas por un número sino por algo llamado el tensor de Ricci.

Un tensor no es más que la extensión del concepto de vector a dimensiones adicionales. Un escalar, un número, aparece en un gráfico como un punto, un objeto de cero dimensiones. Un vector, que tiene magnitud y dirección, aparecería en un gráfico como una línea, es decir, como un objeto de una dimensión. El tensor extiende esta idea a las dimensiones adicionales. Esto podemos interpretarlo como un conjunto de vectores relacionados, moviéndose en múltiples direcciones en un plano.

Lo veremos mejor de otra manera. En vez de pensar en un vector como un conjunto de coordenadas, lo podemos considerar una operación, es decir, un vector lo que haría es asociar una dirección a un número. Lo importante desde el punto de vista matemático es que la operación es lineal y homogénea. Gracias a esto, un vector queda completamente determinado por sus proyecciones en d direcciones, donde d es el número de dimensiones del espacio en el que se define. Por tanto, un vector se puede expresar como un conjunto de números que son en realidad sus proyecciones en un sistema de ejes coordenados.

Un vector es realmente un tensor de rango 1, asocia 1 dirección a un número. Un escalar, es un tensor de rango 0, asocia 0 direcciones a un número. Por tanto un tensor de rango 2 (un tensor ya por derecho propio), asocia dos direcciones arbitrarias a un número. Si quisiéramos expresarlo en términos de las coordenadas, como se hace con los vectores, necesitaríamos d x d números. Para un tensor de rango q, por tanto, necesitaríamos n^q números.

Las ecuaciones de campo

Veamos ahora desde el punto de vista formal las ecuaciones de campo de la relatividad general. Si has llegado leyendo hasta aquí no te asustará demasiado, después de todo no es más que una igualdad tensorial en la que se relacionan un conjunto de tensores 4 x 4 (simétricos, pero en esto no vamos a entrar ahora), para un espaciotiempo de 4 dimensiones.

Donde R_μν es el tensor de curvatura de Ricci del que hablábamos más arriba, R es la curvatura escalar (simplificando, la curvatura entendida en el sentido que hablábamos más arriba, un número asociado a un punto del espacio), g_μν es el tensor métrico (una generalización del campo gravitatorio y principal objeto de interés), G es la constante gravitacional de Newton, c la velocidad de la luz en el vacío y T_μν el tensor de energía-impulso.

Los índices en los tensores son etiquetas, es una forma de llamarlos. En este caso se emplea la notación abstracta de Penrose. Se puede usar cualquier símbolo conveniente para los índices de los tensores. Tradicionalmente, las letras latinas se usan para indicar que se están usando coordenadas espaciales (x, y, z), mientras que las griegas se emplean para indicar coordenadas espaciotemporales (x, y, z, t).

Notas:

[1] Esta entrega de la serie puede saltarse sin pérdida de continuidad.

[2] En lo que sigue nos basamos mayormente en nuestro nuestro “Einstein y…la pizarra del Observatorio del Monte Wilson” Experientia docet 17/12/2010

[3] La importancia de la cronología puede apreciarse en nuestro Desviación de la luz y falsabilidad

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance