Las últimas entradas que he escrito en el Cuaderno de Cultura Científica las he dedicado a novelas contemporáneas relacionadas de alguna manera con las matemáticas. La última entrada, titulada La estructura geométrica de la novela “Un caballero en Moscú”, analizaba la estructura geométrica de la magnífica novela Un caballero en Moscú (Salamandra, 2018), del escritor estadounidense Amor Towles (1964), estructura que Towles introdujo en la novela, no como un juego creativo, sino como una herramienta para marcar el ritmo narrativo de la historia. Por otra parte, la entrada anterior, Los humanos, un Macguffin matemático, mostraba, tomando como ejemplo la divertida novela Los humanos (Roca Editorial, 2014), del escritor británico Matt Haig (1975), que el Macguffin de una película o novela (recordemos que el Macguffin, término acuñado por el maestro del suspense Alfred Hitchcock, es un objeto, persona, situación o suceso necesario para impulsar la trama y la motivación de los personajes, pero insignificante, sin importancia o irrelevante en sí mismo; como diría el cineasta Francois Truffaut “es el pretexto”) también puede ser matemático, en concreto, el Macguffin de esta novela es una supuesta demostración de la hipótesis de Riemann.

En esta entrada vamos a continuar hablando de literatura contemporánea, pero ahora no de una novela, sino de todo un género literario, la novela negra o policiaca.

Las matemáticas en la novela negra

Seguramente el género narrativo que, en la literatura contemporánea, cuenta con una mayor presencia de las matemáticas, sin tener en cuenta la ciencia ficción, sea la ficción criminal, es decir, el género que engloba la novela negra, la novela policiaca y la novela de misterio.

Ya desde los orígenes de la novela policiaca, la serie de relatos del detective Auguste Dupin, el detective creado por el escritor estadounidense Edgar Allan Poe (1809-1849), el lector se encuentra ya una clara referencia a las matemáticas en relación con la inteligencia analítica que posee el detective Dupin y que utiliza para resolver los misterios, así como menciones a áreas de las matemáticas como el análisis matemático, el álgebra o la probabilidad. Más aún, la criptografía juega un papel importante en el relato El escarabajo de oro (1843).

Los relatos del detective Auguste Dupin, al igual que las novelas y relatos de otros míticos detectives, como Sherlock Holmes (creado por el británico Arthur Conan Doyle (1859-1930)), Hércules Poirot, Miss Marple (por la escritora británica Agatha Christie (1890-1976)), el profesor Van Dusen, conocido como la máquina pensante (por el escritor estadounidense Jacques Futrelle (1875-1912)) o D. Isidro Parodi (por los escritores argentinos Jorge Luis Borges (1899-1986), Adolfo Bioy Casares (1914-1999)), entre otros, pertenecen a la escuela inglesa del género policiaco. Esta se caracteriza por centrar la historia en la resolución puramente intelectual del misterio, en muchos casos, un asesinato. El relato se centra en el detective y la resolución del caso policial. Ya Edgar Allan Poe hablaba de estas historias como de “historias de raciocinio”. Es principalmente en esta clase de novelas policiacas donde nos encontramos el paralelismo entre la investigación policial y la matemática, la resolución de un misterio o caso policial, y la de un problema matemático, aunque también nos encontramos con ejemplos de ese paralelismo en toda la ficción criminal.

Los pasos para resolver un caso policial serían, o deberían ser, análogos a los que se realizan para resolver un problema matemático, un juego de ingenio o demostrar un teorema: i) análisis del problema o misterio; ii) búsqueda de estrategias para la resolución; iii) aplicación de la estrategia considerada a partir de la reflexión anterior; iv) si se obtiene una solución, revisarla bien, pero si no resuelve el problema o misterio, volver a los puntos iniciales, pero guardando constancia de lo aprendido; v) aprender y generalizar.

En esta entrada del Cuaderno de Cultura Científica mostraremos como en la ficción criminal actual sigue existiendo una presencia importante de las matemáticas. Sobre algunos ejemplos ya hemos escrito en la sección Matemoción del Cuaderno de Cultura Científica, como La incógnita Newton, de Catherine Shaw (véase la entrada [El problema de los tres cuerpos. Un misterio en Cambridge), La chica que soñaba con una cerilla y un bidón de gasolina, segunda entrega de la serie Millenium, de Stieg Larsson (véase la entrada La chica que soñaba con una cerilla y un bidón de gasolina), La mano del diablo, de Douglas Preston y Lincoln Child (véase Crímenes áureos) o El asesinato de Pitágoras, de Marcos Chicot (véase las entradas El asesinato de Pitágoras, historia y matemáticas (I) y El asesinato de Pitágoras, historia y matemáticas (II)).

Los crímenes de Oxford

Empezaremos nuestro paseo por una conocida novela, que fue todo un bestseller a nivel mundial, traducida a treinta y tres idiomas, la novela Crímenes de Oxford (Destino, 2004), del escritor y matemático argentino Guillermo Martínez.

El entorno, los personajes, el argumento, la estructura y algunos ingredientes de esta novela negra “a la inglesa”, que fue llevada al cine por el cineasta vasco Alex de la Iglesia, rezuman matemáticas, pero integradas perfectamente, sin que al lector pueda sorprenderle su presencia.

La historia tiene lugar en Oxford, a cuyo Instituto de Matemáticas ha ido a estudiar un joven matemático argentino (alter ego del autor de la novela). Este, junto al eminente lógico Arthur Seldom, se ve implicado en la investigación de una serie de asesinatos, que se inician con el de Mrs. Eagleton, casera del joven, amiga del famoso matemático y una de esas mujeres inglesas que durante la segunda guerra mundial ayudaron a Alan Turing a descifrar la máquina enigma. Como es de imaginar estos son algunos de los temas matemáticos que aparecen en la novela, la criptografía, la máquina enigma o el matemático Alan Turing (véase la entrada Alan Turing, un soñador), junto con otros como Pitágoras, el número de oro (véase la entrada ¿Es áureo el Aston Martin de James Bond?), el teorema de Fermat (véase la entrada Euler y el último teorema de Fermat), la demostración de Andrew Wiles (véase la entrada Andrew Wiles: de conjetura a teorema), las sucesiones, el teorema de Wittgenstein o el teorema de incompletitud de Gödel.

El autor de los asesinatos deja en cada uno de ellos un símbolo matemático, círculo, vesica piscis y triángulo, de forma que hay un doble reto intelectual para los protagonistas, saber cómo se continúa la serie matemática y cuál es la regla que sigue –Seldom precisamente ha escrito un libro sobre series lógicas-, y su reflejo en los asesinatos, es decir, cuál es la pauta que sigue el asesino para matar y quien será su siguiente víctima. Finalmente, se descubre que los signos tienen que ver con la secta de los pitagóricos y la sucesión está ligada a los números, 1, 2 y 3, siendo el siguiente la Tetraktys pitagórica (asociada al 4, porque es la suma de los cuatro primeros números), y en paralelo, también al asesino.

Sin embargo, como se explica en el libro, la paradoja de Wittgenstein sobre las reglas finitas establece que dada una sucesión finita de números estos se pueden continuar de muy diversas formas, existiendo reglas que lo justifican, y más aún, puede continuarse realmente con cualquier número, de manera que siempre existirá una regla asociada. Por ejemplo, la serie 2, 4, 8, 16, parece lógico que se deba continuar con el 32, puesto que son potencias de 2, sin embargo, la serie se puede pensar como el número de regiones del círculo en las que este se divide mediante los segmentos que unen un número finito de puntos sobre la circunferencia exterior (2, 3, 4, 5 puntos), entonces el siguiente número de la serie sería 31, y no 32.

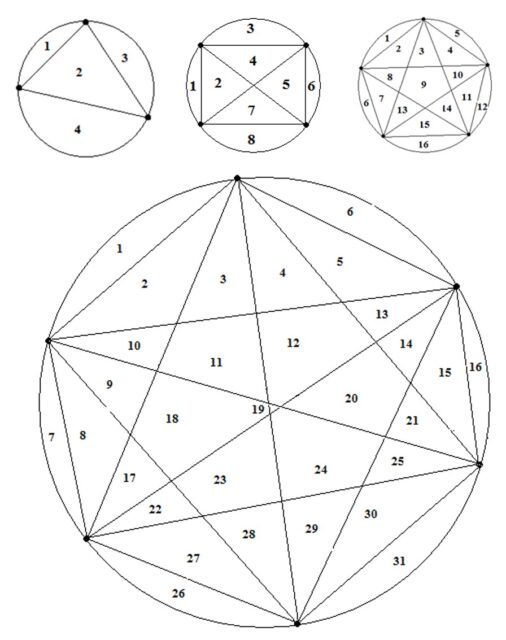
El argumento de la novela sigue en cierta forma la paradoja de Wittgenstein, y en el último capítulo el joven matemático descubre que la serie de asesinatos puede ser explicada de otra forma, y el asesino ser realmente otro.

A lo largo de la narración los dos matemáticos discuten sobre el paralelismo entre la investigación matemática y la desarrollada para resolver un crimen, y se cita el Teorema de Gödel, muy presente en toda la obra, para distinguir entre la verdad y la verdad demostrable.

Guillermo Martínez no solo mantiene la intriga hasta el final de la narración, sino que la adereza de pequeños relatos de misterio de una gran fuerza narrativa, como la historia del matemático Frank Kalman. Además, incluye en la trama de la novela uno de los acontecimientos matemáticos más importantes de las últimas décadas, la presentación de Andrew Wiles de la demostración del Teorema de Fermat, que tuvo lugar en la Universidad de Cambridge en 1994 y apareció en los medios de comunicación de todo el planeta (véase la entrada Los institutos Isaac Newton y Oberwolfach, do scuriosas instituciones de investigación matemática).

La devoción del sospechoso X

En la premiada novela, y éxito de ventas, La devoción del sospechoso X (Ediciones B, 2011), del escritor e ingeniero japonés Keigo Higashino (1958), se produce un duelo intelectual entre dos mentes matemáticas, que nos podría recordar, aunque el tema es completamente distinto, al duelo intelectual entre el detective Sherlock Holmes y su archienemigo James Moriarty, brillante matemático, en particular en la novela El problema final (1893).

Una madre soltera y divorciada acaba matando, junto a su hija, a su acosador ex-marido al complicarse la visita de este, pero en su ayuda aparece su vecino, un profesor de matemáticas de instituto (un genio de las matemáticas que tuvo que abandonar su prometedora carrera universitaria para cuidar a sus padres, aunque sigue centrando su vida en su investigación matemática), que les ayudará a deshacerse del cuerpo y a proporcionarles una cuartada perfecta, haciendo uso para ello de su brillante mente matemática. Pero la policía cuenta con la colaboración de un profesor de física de la Universidad de Tokio, aficionado a las matemáticas y antiguo compañero universitario del anterior, para intentar resolver el crimen, Manabu Yuwaka, conocido como el detective Galileo, protagonista de una serie de novelas policiacas de Higashino.

Como metáfora del duelo intelectual, los dos científicos se plantean la cuestión, “¿Qué es más difícil, elaborar un problema que la gente sea incapaz de resolver o resolverlo?”, y la técnica utilizada por el profesor para despistar a la policía, es la misma que emplea para poner los exámenes en el instituto “simulo que he puesto un problema de geometría, cuando se trata de un problema de funciones”.

En las conversaciones entre los dos científicos aparecen algunos temas matemáticos como el teorema de los cuatro colores y su polémica demostración por ordenador, que rompió la filosofía de las demostraciones clásicas matemáticas (puede verse la serie de entradas dedicadas al problema de los cuatro colores Una historia que comienza en 1852, El error de Kempe y la clave de la prueba, Tras un siglo de aventura … ¿un ordenador resuelve el problema? y ¿Podemos creer la prueba de la conjetura?), el matemático Paul Erdös, el problema “P versus NP” sobre la complejidad computacional, la hipótesis de Riemann, relacionada con la distribución de los números primos (véase la entrada Los humanos, un Macguffin matemático), el lápiz y el papel como herramientas básicas en las matemáticas, la belleza de la resolución de un problema (relacionada con la resolución de problemas de matemáticas pueden leerse las entradas Las dos culturas de las matemáticas: construir teorías o resolver problemas, Un dulce problema de Paul Erdös o El problema del final feliz), o la enseñanza de las matemáticas en un instituto de secundaria y la eterna cuestión de para qué sirven estas.

La brisca del cinco

Otro ejemplo diferente nos lo encontramos en las novelas de la serie del bar BarLume del escritor italiano Marco Malvaldi (1974), que se inicia con La brisca del cinco (Destino, 2012), se continúa con El juego de las tres cartas (Destino, 2012) y El caso del mayordomo asesinado (Destino, 2013), que son las tres novelas de la serie publicadas en España, y otras novelas no traducidas al castellano.

El protagonista de La brisca del cinco es un licenciado en matemáticas que dejó su doctorado (sobre las matemáticas de la teoría de cuerdas) para ganarse la vida con un bar, el BarLume, en el cual se reúnen cuatro ancianos a jugar a las cartas y cuyas charlas con Massimo sirven para desarrollar los argumentos de la investigación criminal. Massimo utiliza su mente matemática para analizar e intentar resolver los crímenes.

De nuevo el paralelismo entre las investigaciones matemática y criminal. Massimo reflexiona sobre que en ambas no basta con saber –o creer saber- la verdad, hay que demostrarla, o explica que “Un axioma es una proposición que se asume como verdadera porque es considerada obvia, y que proporciona el punto de partida para la construcción de un sistema matemático” y “no es posible demostrar” su validez, y se alude también al teorema de Gödel, pero en su investigación ha asumido como una verdad inicial, un axioma, algo que no lo era y eso le impedía descubrir al asesino.

Además, hay continuas alusiones a las matemáticas (el uso frecuente de expresiones como “dos más dos son cuatro” para transmitir que algo es obvio o que ha llegado a una conclusión, la pasión de los matemáticos por el café, el chiste de las ovejas en Escocia (sobre chistes matemáticos pueden leerse las entradas ¿Saben aquel que dice … matemáticas? (I) y ¿Saben aquel que dice … matemáticas? (II), las permutaciones (sobre permutaciones hay muchas entradas, dos de ellas podrían ser La ratonera, el juego de Cayley y El problema matemático de las cartas extraviadas) o la capacidad computacional de los ordenadores) o a la ciencia en general (congresos científicos, situación de la ciencia italiana, Newton, Fermi o Einstein).

Los crímenes del número primo

Otra novela policiaca en la que nos encontramos un personaje que ha dejado las matemáticas para dedicarse a otra cosa, en este caso, para ser fraile, es la novela Los crímenes del número primo (RBA, 2008), de la escritora y economista Reyes Calderón (1961), y posteriores libros de la jueza MacHor.

En Los crímenes del número primo, primera entrega de las aventuras de la jueza Lola MacHor y el inspector de la interpol Juan Iturri, estos investigan los asesinatos del arzobispo de Pamplona y el abad del monasterio de Leyre. El asesino deja una nota con el número 3313, y el hermano Chocarro (que era un genio de las matemáticas, “un nuevo Einstein”, que había investigado en ecuaciones diferenciales, simulación, teoría de juegos o la distribución de los números primos, pero las abandonó para ordenarse a fraile) observa que es un número primo. ¿Y qué tienen que ver estos con la iglesia y los crímenes?

Como explica el fraile, el teólogo suizo Hans Urs von Balthasar (1905-1988) realizó una comparación entre ciertos santos de la iglesia y los números primos. Según él, había dos tipos de santidad, la que va de Dios a la Iglesia, y la que va de esta a Dios, y es la primera la que recoge los deseos de Dios y es capaz de guiar a la Iglesia y a la humanidad. “Estos santos se presentan como piedras angulares de la Iglesia y a ellos llama Baltasar números primos, puros, impredecibles, directamente venidos del cielo”. El asesino se reconoce como un número primo (3313), que debe de matar al arzobispo y al abad (que quizás podrían considerarse números primos) “para cambiar lo que ellos han hecho mal”.

Por otra parte, esta novela, y otras de la serie de la jueza MacHor, están salpicadas de pequeñas referencias a las matemáticas, algunas más bien metafóricas, o incluso cuyo significado es dudoso, y otras más ancladas en lo real (probabilidad, azar, estadística, campana de Gauss). En cualquier caso, tienen como positivo que presentan a las matemáticas formando parte de la vida cotidiana. Aunque se presenta a la jueza como una persona alérgica a las matemáticas, “Es usted el agente Iturri de la Interpol o me han pasado con el profesor de matemáticas” o “Lo siento hermano, yo soy de letras. Las ecuaciones, funciones o curvas me dan alergia”, está rodeada de personas más afines a ellas, como el fraile Chocarro (genio de las matemáticas, del que tenemos la cita, “la ciencia matemática enseña a resolver problemas complejos. Lo más importante, por supuesto, es la resolución, pero también se consideran la elegancia y la eficiencia con que se llega a ésta. Una solución en tres pasos es siempre mejor que una en seis”), el agente Iturri (que confía en ellas) o su marido, científico, y su hijo de 10 años (que adoran las matemáticas).

Sé lo que estás pensando

La novela Sé lo que estás pensando (Roca, 2010), del escritor estadounidense John Verdon (1942), es un thriller que se inspira en una sencilla cuestión de teoría de probabilidad, similar al “timo bursátil” del matemático John Allen Paulos en El hombre anumérico (Tusquets, 1990), como desencadenante de una trama con varios asesinatos que serán investigados por el detective Gurney. La historia empieza con un hombre que recibe una carta en la que se le pide que piense en un número del 1 al 1.000, tras lo cual abre un sobre que venía en la carta y descubre que está escrito el número que está pensado en ese momento. Días más tarde morirá asesinado y se iniciará la investigación de su muerte. La adivinación de su número no es una cuestión de magia, sino de probabilidad. No vamos a explicarlo, al menos en esta ocasión, para no desvelar el secreto a las personas que puedan leerlo a partir de esta entrada.

Podríamos continuar con muchos más ejemplos de ficción criminal en las que se incluyen las matemáticas, pero para esta entrada ya son suficientes ejemplos. Eso sí, os animo a que los leáis y disfrutéis tanto de la parte literaria, como de la matemática.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica